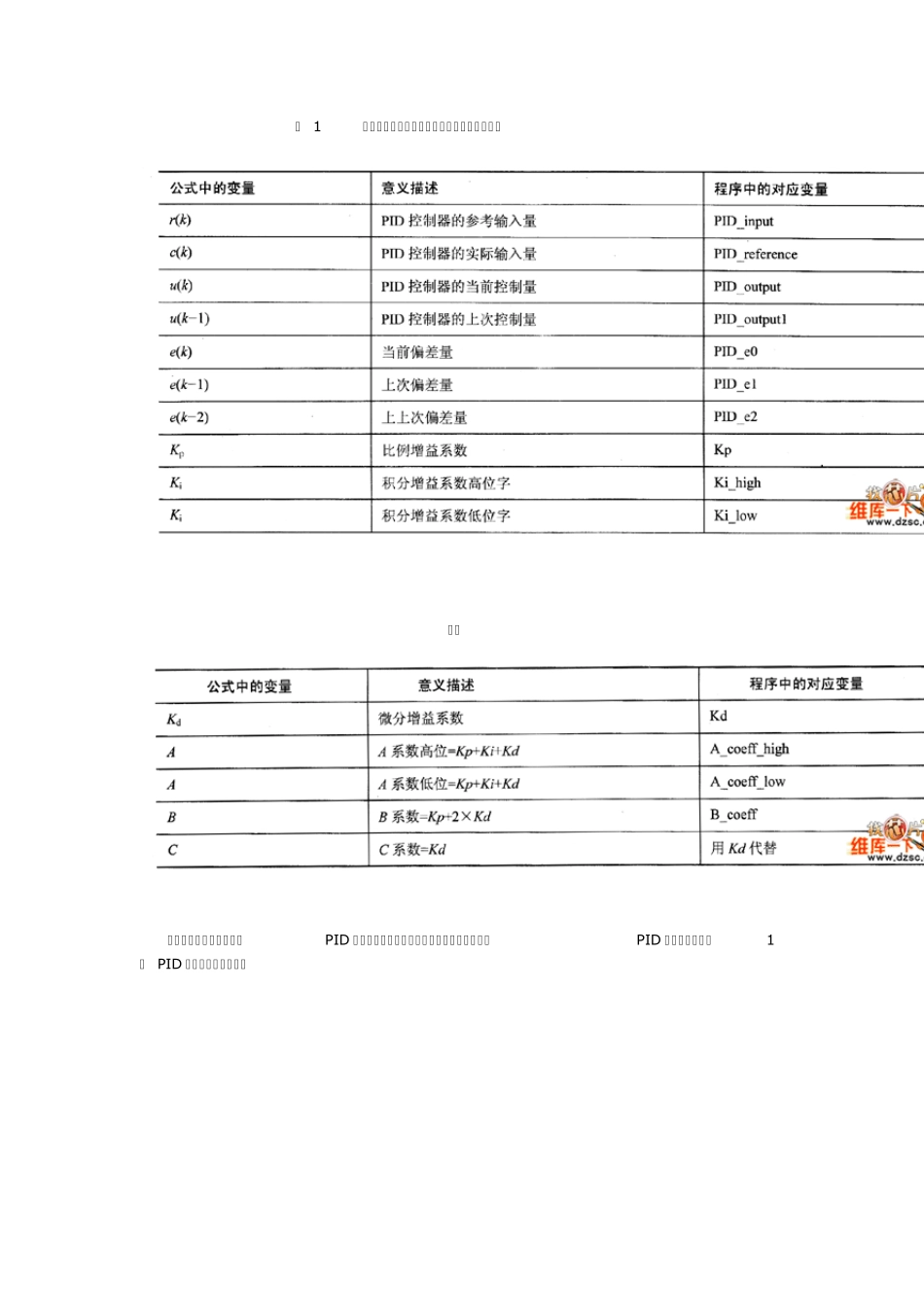
表 1 公式中变量和程序中变量的对应关系及意义表 续表 本案例首先设计一个数字P ID 控制器,现在假设它是一个对电动机速度进行P ID 控制的系统。图1是 P ID 控制器的原理框图。 图 1 PID 控制器的原理框图 图 1 中,r(t)是电机速度设定值,c(t)是电机转速的实际测量值,e(t)是输入控制器的偏差信号,勿⑺是控制器输出的控制量,则PID 控制算式如式4- 1 所示。 在式4-1 中,Kp 是比例系数,起比例调整作用。Ti 是积分时间常数,它决定了积分作用的强弱。Td是微分时间常数,它决定了微分作用的强弱。在PID 控制的3 种作用中,比例作用可对系统的偏差做出及时响应;积分作用主要用来消除系统静差,改善系统的静态特性,体现了系统的静态性能指标;微分作用主要用来减少动态超调,克服系统振荡,加快系统的动态响应,改善系统的动态特性。,PID 控制的3 种作用(比例、积分、微分)是各自独立的,可以分别使用,也可以结合徒用,但是积分控制和微分控制不能单独使用,必须和比例控制结合起来,形成Pl 控制器或者PD 控制器。式4- 1 是模拟形式的PID 控制算式,现在采用LF2407 实现数字PID 控制,则对式4-1 离散化,得到PID 控制的离散形式,如式4- 2所示。 其中Ts 为采样周期。这是位置式PID 控制算式,为了增加控制系统的可靠性,采用增量式PID 控制算式,即让LF2407 只输出控制量u (k)的增量ΔU(k)。式4-2 是第k 次 PID 控制器的输出量,那么第k- 1 次 PID 控制器的输出量如式4- 3 所示。 方程式4-5 就是本控制程序中用到的增量式PID 控制算式。增量式PID 控制与位置式ΠD控制相比仅是算法上有所改变,但是它只输出增量,减少了DSP 误操作时对控制系统的影响,而且不会产生积分失控。本案例基于LF2407 的 PID 控制器的实现框图如图2 所示。 图 2 基于LF24O7 的 PID 控制器的实现框图 从图2 可以看出被控电机的速度设定量由DSP 给出,经过DSP 计算出控制量u ( k),对它进行DA转换,产生模拟控制量u ( t),从而实现对被控电机速度的控制,而电机实际转速c( t)通过AD 转换器送入DSP,使整个系统构成一个闭环系统。如图3 所示是本案例设计的数字PID 控制器在DSP 上实现的控制程序流程图。 图 3 基于LF24O7 的数字PID 控制器的程序流程图 其次,本案例还要设计一个模糊PI 控制器,它的硬件电路如图2 所示,和数字PID 控制器的硬件电路是一样的。...