数字信号处理(合成地震记录amp;fft)

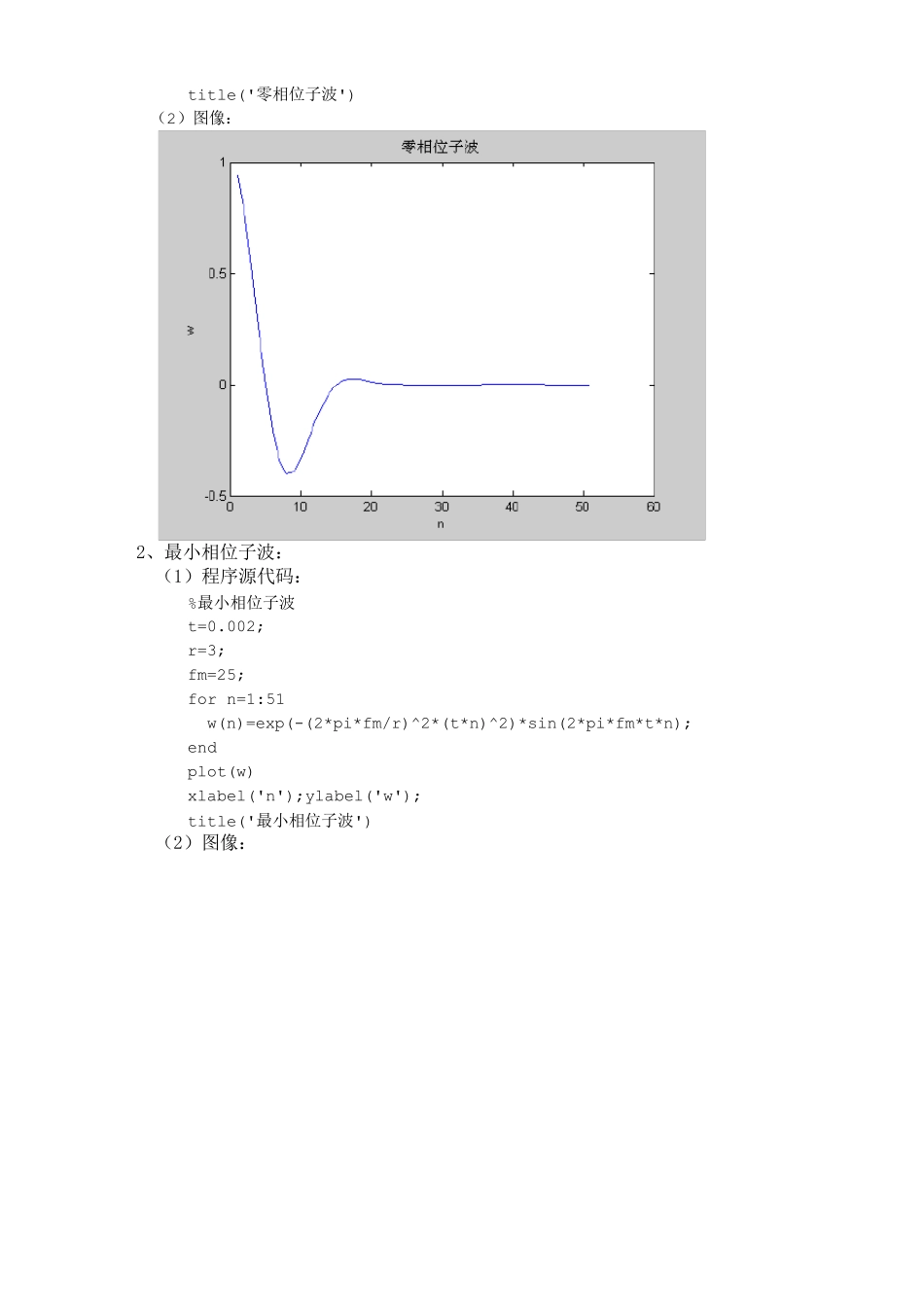
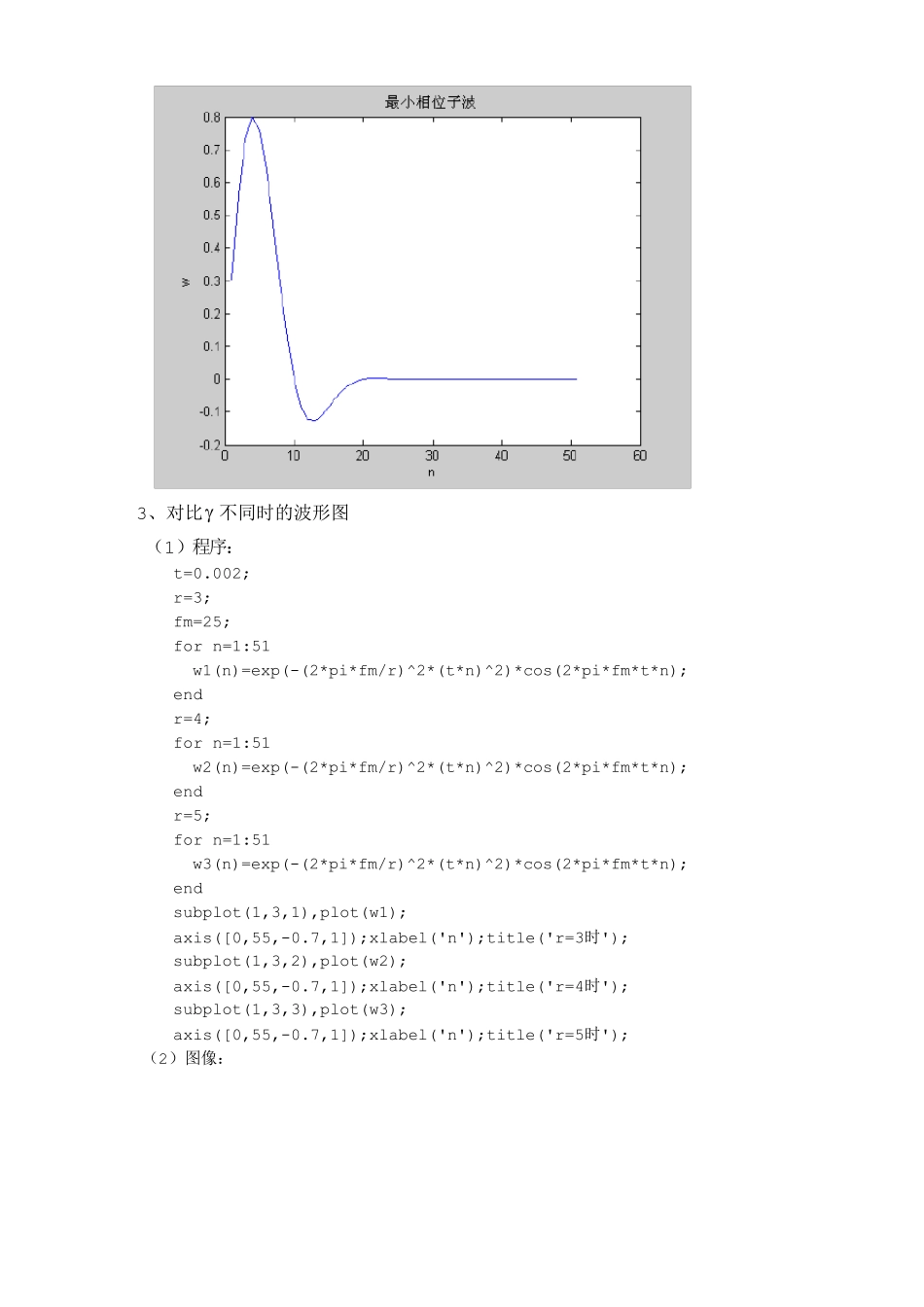
数字信号处理实验报告 实验一、地震子波波形显示及一维地震记录合成 一、实验目的 1、认识地震子波（以雷克子波为例），对子波有直观的认识。 2、利用线性褶积公式合成一维地震记录。 二、实验内容 1、 雷克子波：  tfetwmtf m2cos22/2（零相位子波）、  tfetwmtf m2sin22/2（最小相位子波）， 其中mf 代表子波的中心频率，  代表子波宽度 ,随着 的增大，子波能量后移，当 =7 时，最小相位子波可视为混合相位子波，这里取mf = 25 Hz ， = 3; 2、 根据公式编程实现零相位子波、最小相位子波的波形显示； 3、 设计反射系数)(nr(n=500) ，其中0.1)100(r，7.0)200(r，5.0)300(r，4.0)400(r，6.0)500(r，其它为 0; 4、 应用褶积公式Nmmnwmrnwnrnf1)()()()()(合成一维地震记录，并图形显示； 5、 根据所学知识对实验结果进行分析。 三、实验结果： 1、零相位子波： （1）程序源代码： %编写零相位子波 t=0.002; r=3; fm=25; for n=1:51 w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n); end plot(w) xlabel('n') ylabel('w') title('零相位子波') （2）图像： 2、最小相位子波： （1）程序源代码： %最小相位子波 t=0.002; r=3; fm=25; for n=1:51 w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*sin(2*pi*fm*t*n); end plot(w) xlabel('n');ylabel('w'); title('最小相位子波') （2）图像： 3、对比 不同时的波形图 （1）程序： t=0.002; r=3; fm=25; for n=1:51 w1(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n); end r=4; for n=1:51 w2(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n); end r=5; for n=1:51 w3(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n); end subplot(1,3,1),plot(w1); axis([0,55,-0.7,1]);xlabel('n');title('r=3时'); subplot(1,3,2),plot(w2); axis([0,55,-0.7,1]);xlabel('n');title('r=4时'); subplot(1,3,3),plot(w3); axis([0,55,-0.7,1]);xlabel('n');title('r=5时'); （2）图像： （3）分析：  代表子波宽度，随着 的增大，子波能量后移。 4、一维地震记录： （1）零相位子波程序： t=0.002; r=3; fm=25; for n=1:51 w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n); end %设置反射系数 r=zeros(500); r(100)=1.0;...