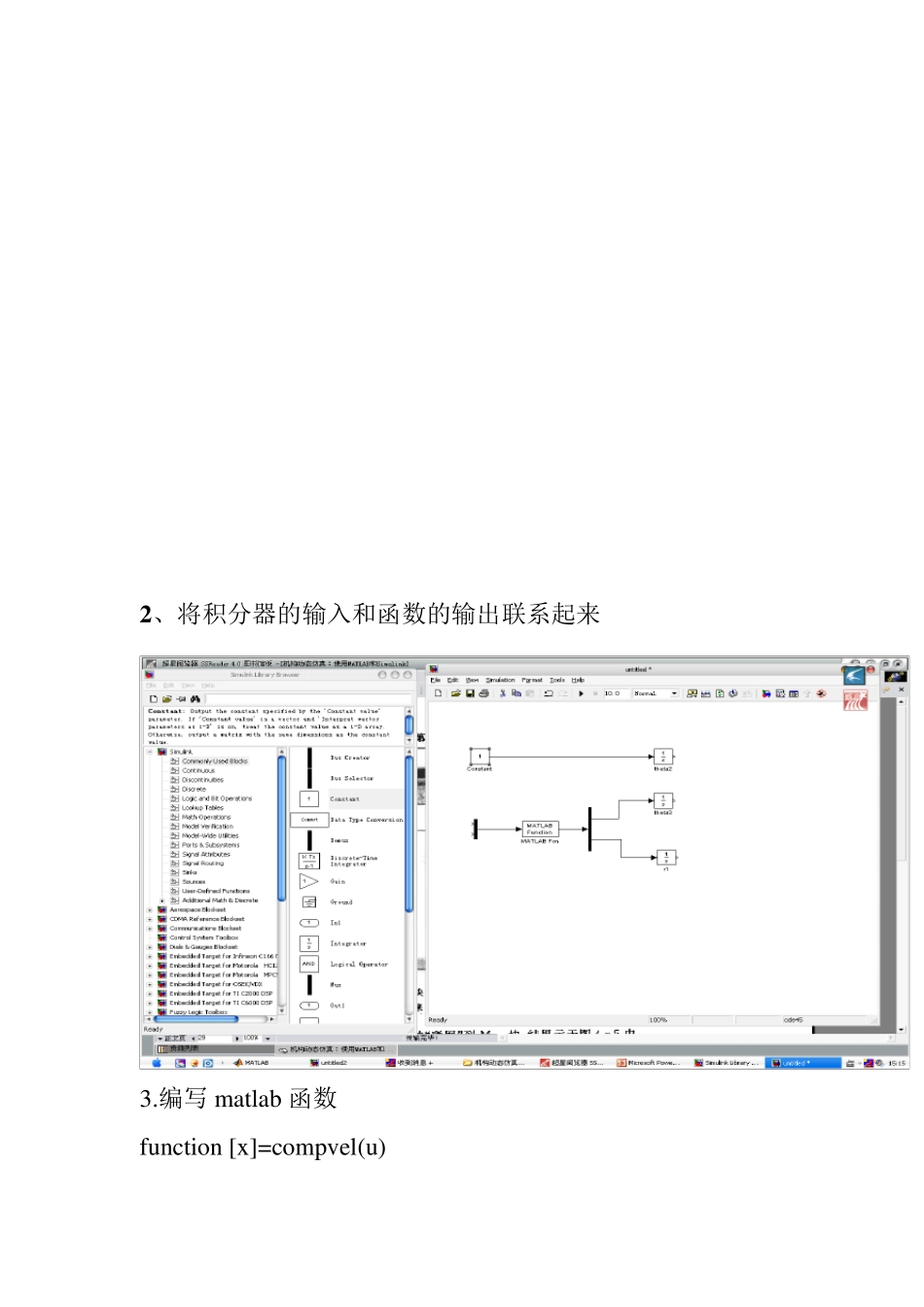
曲柄滑块结构的simu link 仿真 一、 曲柄滑缺机构的闭环矢量方程 为了说明这种方法,对一个曲柄以匀速旋转若干困的曲柄滑块机构进行运动学仿真分析。图4—1 给出了曲柄滑块机构的示意图。通常,单缸四冲程发动机中就有这种机构。 图4—2 结出了描述曲柄滑块机构的矢量环。对于曲柄滑块机构,矢量x1 的大小随时间变化,而方向保持不变。这一点在计算对时间的导数时是非常重要的。 曲柄滑块机构的闭环矢量方程为 将此矢量方程分解到 z 和 y 坐标轴上,得到 将上式对时间求导数,有 其中是矢量大小的变化率,也是滑块相对于地面的平移速度。可以写成如下的矩阵形式: 如果曲柄的速度omega2 已知,方程描述的是曲柄滑块机构速度问题。 二、 曲柄滑块结构的simu link 仿真 当 Omega2 和连杆 2 的长度已知,通过 可求出 omega3 和 dr1.如果将omega2 作为仿真输入,可以用数值积分从速度中求出 theta2,theta3,r1。 1、在面向模块的simu link 仿真中,实现这一过程需要三个积分模块作为仿真的开始。 2、将积分器的输入和函数的输出联系起来 3.编写 matlab 函数 fu nction [x ]=compv el(u ) %u (1)=omega-2 %u (2)=theta-2 %u (3)=theta-3 % r2=1.0; r3=4.0; % a=[r3*sin(u (3)) 1;-r3*cos(u (3)) 0]; b=[-12*u (1)*sin(u (2));r2*u (1)*cos(u (2))]; % x =inv (a)*b; 4、将适当的信号和函数的输入联系起来 5.匀速输入时完成的运动学仿真 6、建立初始条件 在仿真运行之前,必须为积分器建立初始条件。这是求解任何微分方程的关键一步,而且,这对于运动学仿真显得特别重要。如果使用了不相容的初始条件,就会导致仿真失败。Theta2、theta3、r1 必须是机构某个真实位置时的角度和长度。 假设仿真的初始条件: Theta2=0rad;theta3=0rad;r1=177mm 7、运行仿真结果 输入: Th20=0; Th30=0; R10=177; Plot(tou t,simou t(:,5))