抛物线的简单几何性质位置VIP免费

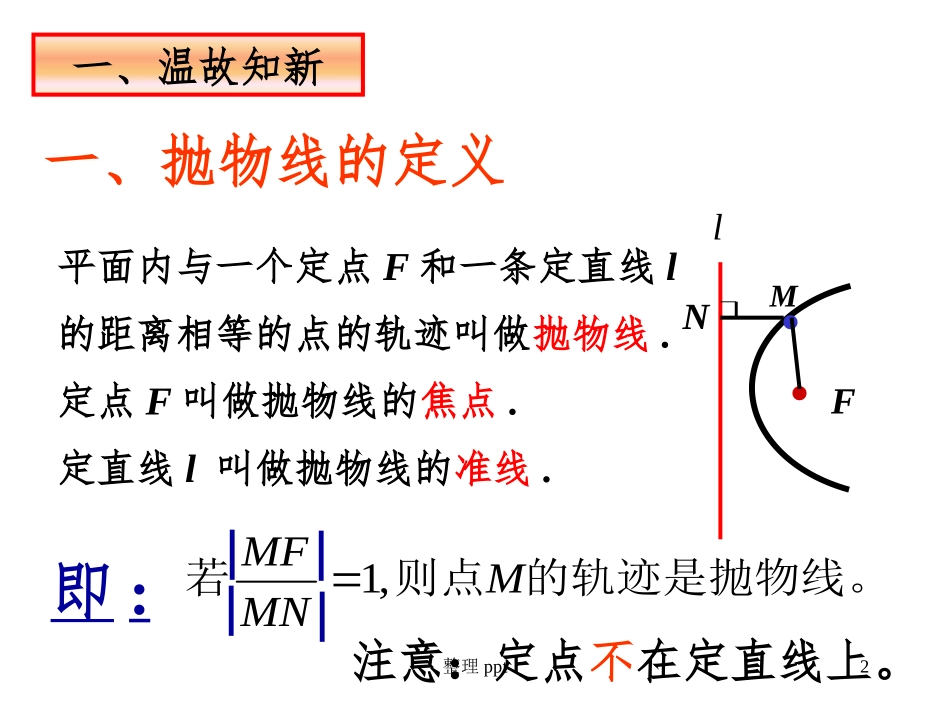
1抛物线的几何性质整理ppt2平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的焦点.定直线l叫做抛物线的准线.一、抛物线的定义的轨迹是抛物线。则点若MMNMF,1即:︳︳︳︳··FMlN注意：定点不在定直线上。一、温故知新整理ppt3102341.:,..,..:..:..xyRxe范围关于轴对称我们把抛一物线的对称轴叫做抛物线的轴顶点坐标原点离心抛物线的简单率性质KFOxy整理ppt4(二）抛物线标准方程及简单几何性质图形方程焦点准线范围顶点对称轴elFyxOlFyxOlFyxOlFyxOy2=2px（p>0）y2=-2px（p>0）x2=2py（p>0）x2=-2py（p>0）)0,2(pF)0,2(pF)2,0(pF)2,0(pF2px2px2py2pyx≥0yR∈x≤0yR∈y≥0xR∈y≤0xR∈(0,0)x轴y轴1整理ppt5因为抛物线关于x轴对称，它的顶点在坐标原点，并且经过点M（２，），22解:所以设方程为：)0(22ppxy又因为点M在抛物线上：所以：2(22)22p2p因此所求抛物线标准方程为：24yx例１：已知抛物线关于x轴对称，它的顶点在坐标原点，并且经过点M（２，），求它的标准方程.22三、典例精析坐标轴当焦点在x(y)轴上,开口方向不定时,设为y2=2mx(m≠0)(x2=2my(m≠0)),可避免讨论整理ppt62002,,,||.MxyypxFMF设是抛物线上的任一点是其焦点求思考：KFOxyM整理ppt70020202020122222322422,.(),||;(),||-(),||(),|-.|PxypypxPFxpypxPFxpxpyPFypxpyPFy二抛物线的焦半径抛物线上一点与焦点的连线叫抛物线的焦半径整理ppt82322(,),:MPyxF已知为抛物线上一点,为抛练习物线的焦点332,22（，）2,_________.PP（1）若到焦点的距离为则点坐标标为2()_________.PMPFP+的最小值为________，此时点坐标标为72整理ppt9KFOxyAB214,,,.yxABAB斜率为的直线过抛物线的焦点与抛物线交于两点求线段练：的长习211221212221212121211610611148222628:,:(,),(,),,,||():||()()AByxxxAxyBxyxxxxABxxxxppABxxxxp解法直线的方程为代入抛物线方程得设则解法整理ppt10KFOxyAB214,,,.yxABAB斜率为的直线过抛物线的焦点与抛物线交于两点求线段练：的长习211221212221212121211610611148222628:,:(,),(,),,,||():||()()AByxxxAxyBxyxxxxABxxxxppABxxxxp解法直线的方程为代入抛物线方程得设则解法整理ppt11112221221221221212223242,,,,,(),||;(),||(),|.|(),||AxyBxyypxABxxpypxABpxxxpyAByypxpyABpyy过抛物线焦点的弦叫焦点弦设焦点弦端点则三抛物线的焦点弦整理ppt1221122230,,,.:||.()ypxpFlAxyBxyAB已知过抛物线的焦点的直线例抛物线的焦点弦问题问交抛物线于两点求证题1:121222:()()ABAFBFppxxxxp解12xxp整理ppt132112222121224340,,.():,.:,.ypxpFlAxyBxypxxyyp已知过抛物线的焦点的直线交抛物线于两点求证例抛物线的焦点弦问题问题212221212221212222244:,,,()yypyyxxppyyPxxP解由问题的解法知:整理ppt142112211111120133624,,,.():.(),,;(),,;(),;(),;ypxpFlAxyBxyAOBBOAAOBBBxBOAAAx已知过抛物线的焦点的直线交抛物线于两点三点共线三点共线设直线与准线交于则平行轴设直例抛物线的焦点弦问题线与准线交于则平行题轴问11112221112212221222222234:,,,,,,.(),(),().oAoBoAoByyyypkkpyxyppypyypkkppyAOB解而三点共线同理可证整理ppt15211223207.(),,,.::ypxpFlAxyBxyAB已知过抛物线的焦点的直线交抛物线于两点求证例抛物以为直线的焦径的圆点弦与问题问题准线相切111111222:,,,,,,,.ABMABMABMAABBAFBFABMM解设的中点为过分别作准线的垂线垂足分别为则结论得证整理ppt16（三）直线与椭圆的位置关系几何角度1)相离2)相切3)相交1）相离直线和椭圆没有交点2）相切直线和椭圆有且只有一个交点3）相交直线和椭圆有两个交点Oxy直线与椭圆的位置...