试验9最短路径问题VIP专享

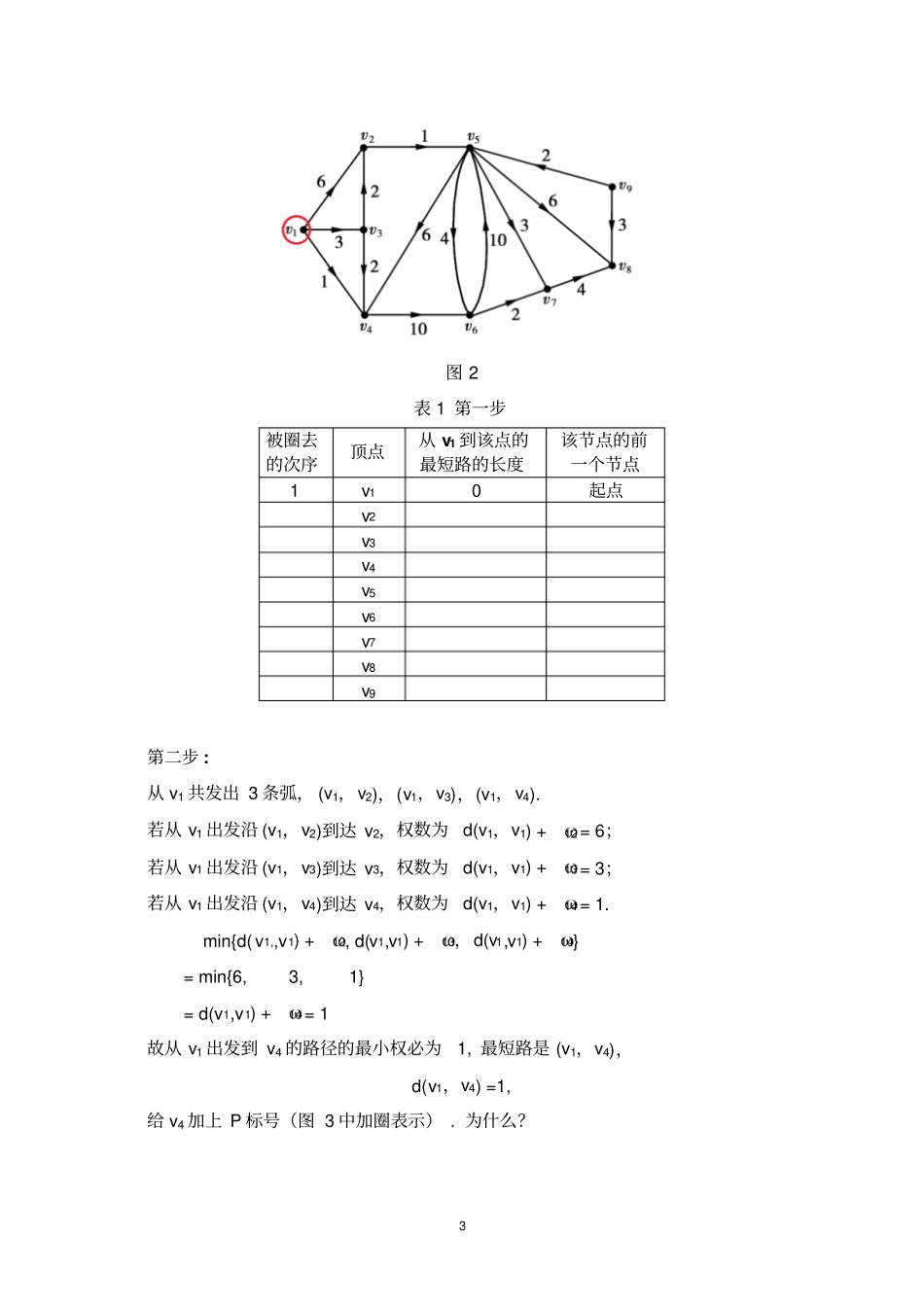
1 实验九最短路径问题及解法一、实验目的1. 了解求解最短路径的Dijkstra 算法和 Floyd 算法的基本原理；2. 掌握 Dijkstra 算法和 Floyd 算法的基本步骤；3. 能应用相关的算法求解实际问题4．掌握 Dijkstra 算法和 Floyd 算法的 C 程序设计技巧；二、实验内容1. 求解最短路径的 Dijkstra 算法及 C 程序实现2. 求解最短路径的 Floyd 算法及 C 程序实现2 1. 求解最短路径问题的Dijkstra 算法问题 1： 已知如图 1 所示的单行线交通网 , 它是一个有向图，每条弧旁的数字表示这条单行线的长度 . 现在某人要从1v 出发，通过这个交通网到8v 去，求使下图中总路程最小的路径 . 图 1 引入基本变量 : ωij: 各边的权数，d(v1，vj)：v1到 vj 的路的总权数的最小值P 标号：从 v1 到 vj 的最短路径的权数已确定T 标号：从 v1 到 vj 的最短路径的权数的上界Si: 算法进行到第i 步时，具 P 标号点的集合 . λ (v)=m：从 vs 到 v 的最短路上， v 的前一个点是 vm, λ (v)=0，则 v=vs. λ (v) =M：D 中不含从 vs 到 v 的路；1.1 结合图表演示 Dijkstra 算法的基本步骤和基本原理我们用图表结全的方法讲述Dijkstra 算法的基本步骤第一步因 ωij≥0，故 d(v1，v1)=0. v1 加上 P 标号（图 2 中用划圈表示） . 3 图 2 表 1 第一步被圈去的次序顶点从 v1 到该点的最短路的长度该节点的前一个节点1v10 起点v2v3v4v5v6v7v8v9第二步 : 从 v1 共发出 3 条弧， (v1，v2)，(v1，v3)，(v1，v4). 若从 v1 出发沿 (v1，v2)到达 v2，权数为d(v1，v1) + ω12 = 6；若从 v1 出发沿 (v1，v3)到达 v3，权数为d(v1，v1) + ω13 = 3；若从 v1 出发沿 (v1，v4)到达 v4，权数为d(v1，v1) + ω14 = 1. min{d( v1,,v1) + ω12, d(v1,v1) + ω13，d(v1,v1) + ω14} = min{6, 3, 1} = d(v1,v1) + ω14 = 1 故从 v1 出发到 v4 的路径的最小权必为1, 最短路是 (v1，v4)，d(v1，v4) =1, 给 v4 加上 P 标号（图 3 中加圈表示） . 为什么？4 图 3 表 2 第二步加 P 标号的次序顶点从 v1 到该点的最短路的长度该节点的前一个节点1 v10 起点v26 v1v33 v12 v41 v1v5v6v7v8v9第三步 : 加上红圈的点表示具有P 标号 , 现考查从 v1 及 v4 指向其余点的弧从 v1 出发，分别沿 (v1，v2)、(v1，v3)到...