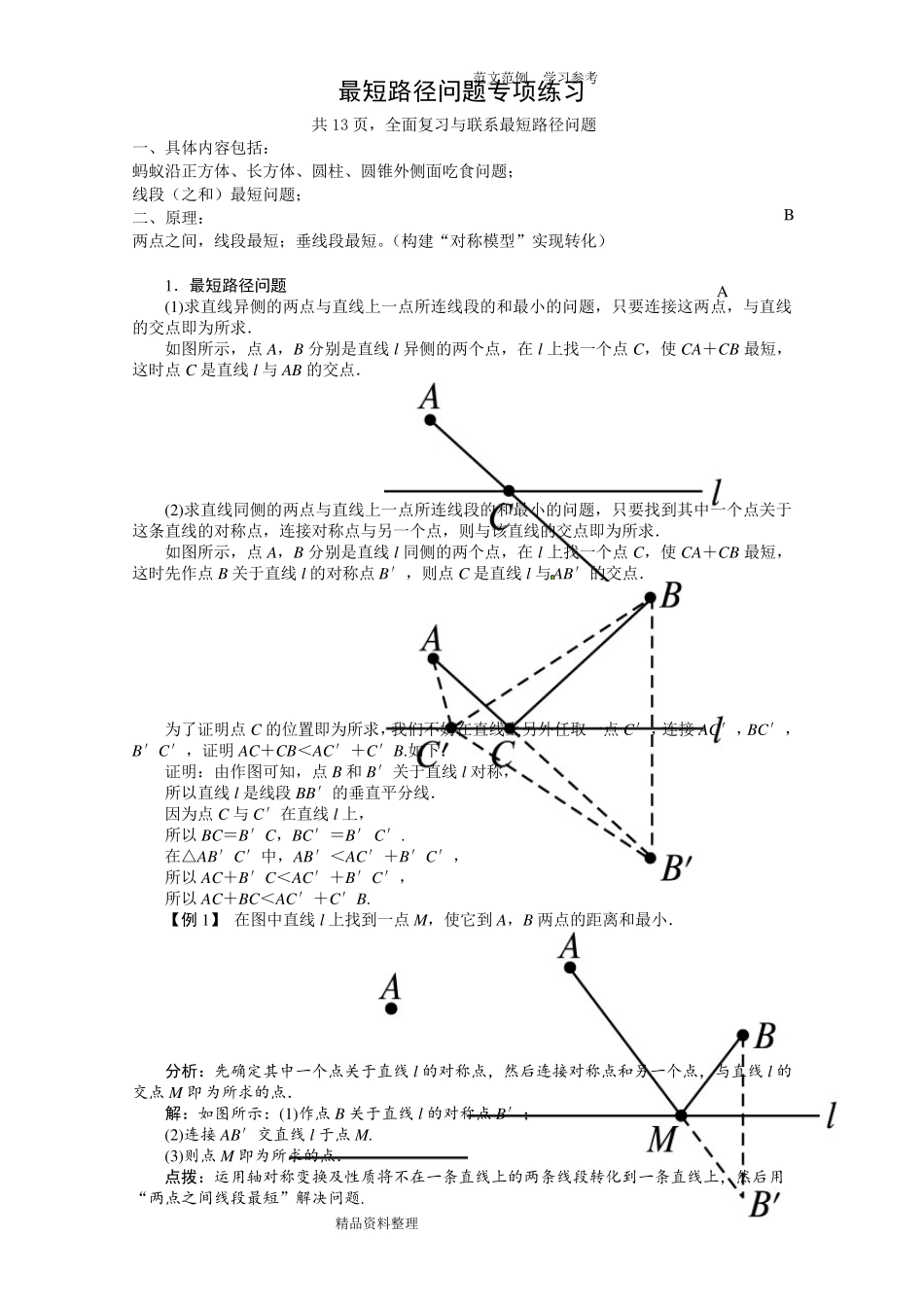
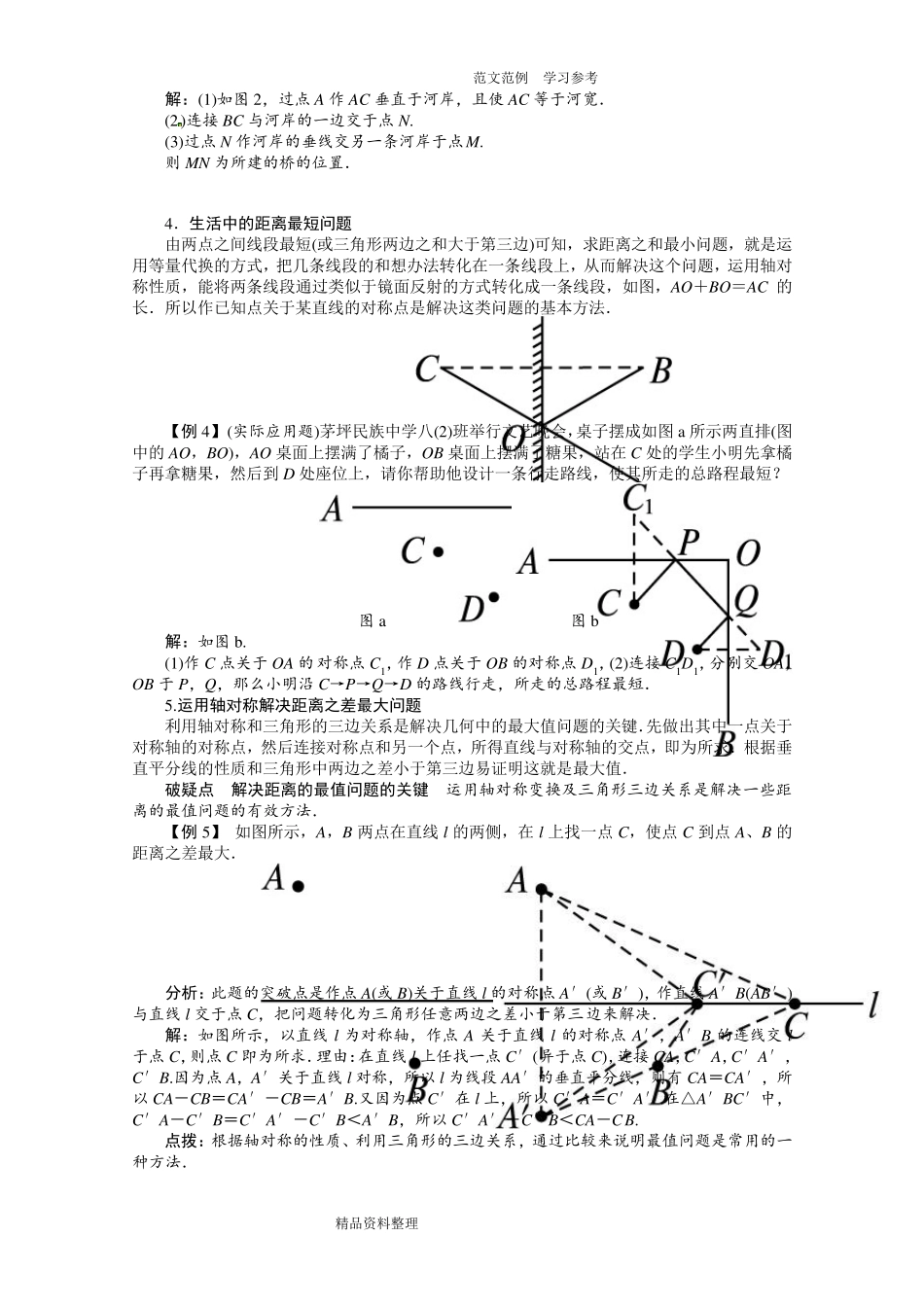
范文范例 学习参考 精品资料整理 A B 最短路径问题专项练习 共13 页,全面复习与联系最短路径问题 一、具体内容包括: 蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题; 线段(之和)最短问题; 二、原理: 两点之间,线段最短;垂线段最短。(构建“对称模型”实现转化) 1.最短路径问题 (1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求. 如图所示,点A,B 分别是直线l异侧的两个点,在 l上找一个点C,使 CA+CB 最短,这时点C 是直线l与AB 的交点. (2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求. 如图所示,点A,B 分别是直线l同侧的两个点,在 l上找一个点C,使 CA+CB 最短,这时先作点B 关于直线l的对称点B′,则点C 是直线l与AB′的交点. 为了证明点C 的位置即为所求,我们不妨在直线上另外任取一点C′,连接 AC′,BC′,B′C′,证明 AC+CB<AC′+C′B.如下: 证明:由作图可知,点B 和B′关于直线l对称, 所以直线l是线段BB′的垂直平分线. 因为点C 与C′在直线l上, 所以 BC=B′C,BC′=B′C′. 在△AB′C′中,AB′<AC′+B′C′, 所以 AC+B′C<AC′+B′C′, 所以 AC+BC<AC′+C′B. 【例 1】 在图中直线l上找到一点M,使它到 A,B 两点的距离和最小. 分析:先确定其中一个点关于直线 l的对称点,然后连接对称点和另一个点,与直线 l的交点 M 即为所求的点. 解:如图所示:(1)作点 B 关于直线 l的对称点 B′; (2)连接 AB′交直线 l于点 M. (3)则点 M 即为所求的点. 点拨:运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上,然后用“两点之间线段最短”解决问题. 范文范例 学习参考 精品资料整理 2 .运用轴对称解决距离最短问题 运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点 到直线上某点的距离和最小这个核心,所有作法都相同. 警误区 利用轴对称解决最值问题应注意题目要求 根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,审...