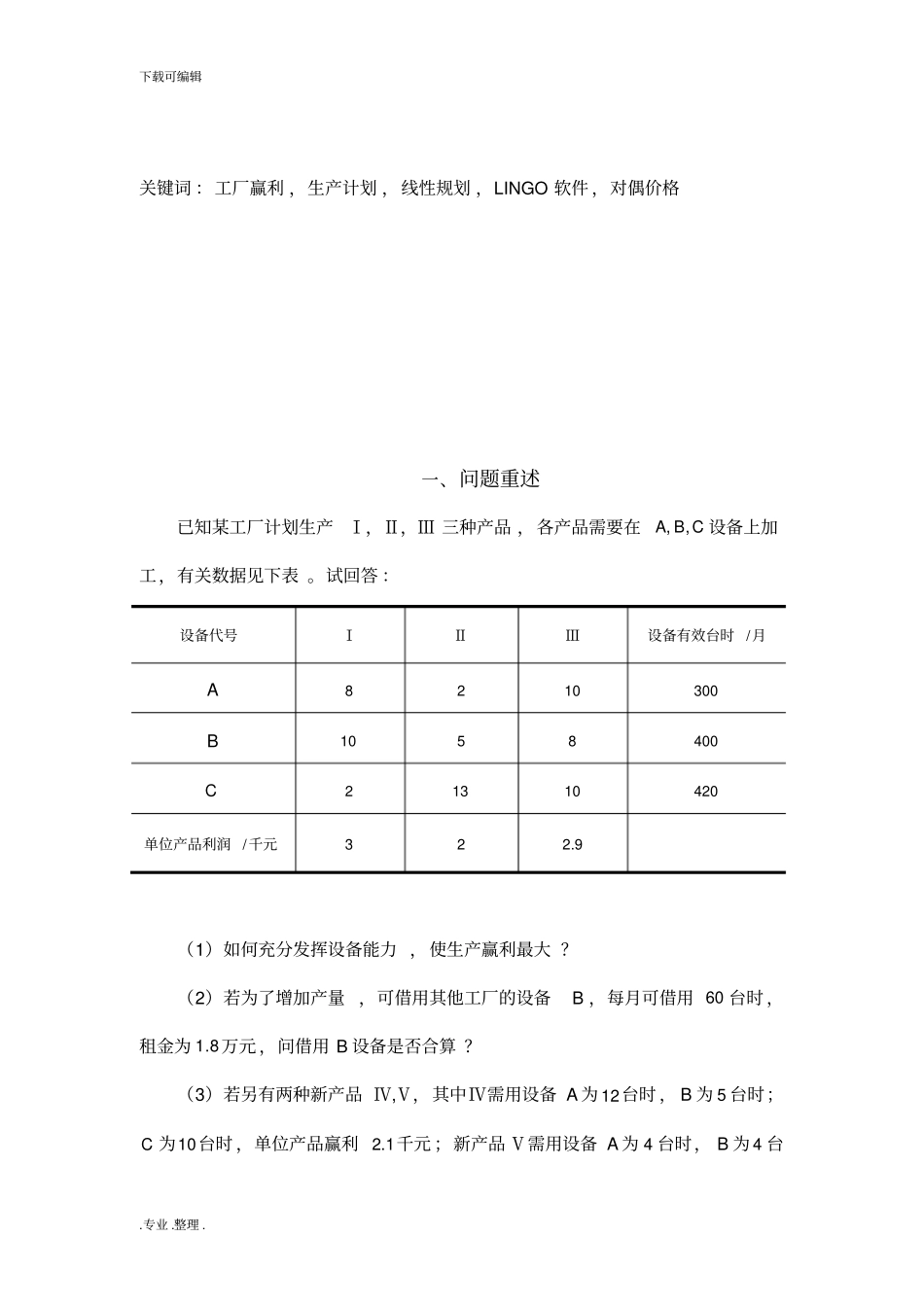
关于生产计划的线性规划模型摘 要本文利用问题中的数据信息,建立了线性规划模型 ,并运用 LINGO 软件求解,得出了让工厂赢利最大的生产计划,并讨论了增加设备 、投产新产品 、改进产品工艺等各种情况对生产计划的影响。对于问题 (1): 按照题目给出的数据 ,可以得到一个每月生产赢利最大为目标的线性规划模型 。然后利用 LINGO 软件求解出模型的全局最优解,最优值为 134.5,最优解为52424321xxx,,。即每月安排生产24 件产品 Ⅰ,24件产品 Ⅱ,5 件产品 Ⅲ,能使工厂获得最大赢利为134.5 千元。对于问题 ( 2): 因为设备 B 每台时的租金为0.3 千元 ,高于它的对偶价格,所以得出结论 :借用设备 B 是不合算的 。我们又建立了线性规划模型来验证结论 。模型计算结果显示借用设备B ,工厂最大赢利为127 千元,比原生产计划下的赢利 134.5 千元少 ,证明了借用设备 B 确实是不合算的 。对于问题 (3): 为了更好的讨论新产品 Ⅳ、Ⅴ 投产是否合算 ,我们分三种情况建立模型 : 同时投产 Ⅳ和Ⅴ、只投产 Ⅳ、 只投产 Ⅴ。 结合三个模型的结果可知 :若单独投产 Ⅳ或Ⅴ,工厂赢利的增量分别是0.1 千元和 1.36 千元。只投产Ⅳ则利润增长是很小的 ,同时投产 Ⅳ和Ⅴ的收益增量是最大的 ,为 1.46 千元。所以在计划新产品的投产时,不能单独投产新产品Ⅳ,最好是同时投产新产品Ⅳ和Ⅴ。对于问题 (4): 根据新数据 ,可以得到线性规划模型 ,模型的最优解为22422321xxx,,。改进工艺结构后最大赢利为152.8 千元 ,给工厂增加了 18.3 千元的赢利 。下载可编辑.专业 .整理 . 关键词 :工厂赢利 ,生产计划 ,线性规划 ,LINGO 软件 ,对偶价格一、问题重述已知某工厂计划生产Ⅰ,Ⅱ,Ⅲ 三种产品 ,各产品需要在CBA,,设备上加工,有关数据见下表 。试回答 :(1)如何充分发挥设备能力 ,使生产赢利最大 ?(2)若为了增加产量 ,可借用其他工厂的设备B ,每月可借用 60 台时 ,租金为8.1万元 ,问借用 B 设备是否合算 ?(3)若另有两种新产品 Ⅳ,Ⅴ,其中Ⅳ需用设备 A 为 12台时 , B 为 5 台时;C 为10台时 ,单位产品赢利1.2千元 ;新产品 Ⅴ需用设备 A 为 4 台时, B 为 4 台设备代号ⅠⅡⅢ设备有效台时 /月A8 2 10 300 B10 5 8 400 C2 13 10 420 单位产品利润 /千元3 2 2.9 下载可编辑.专业 .整理...