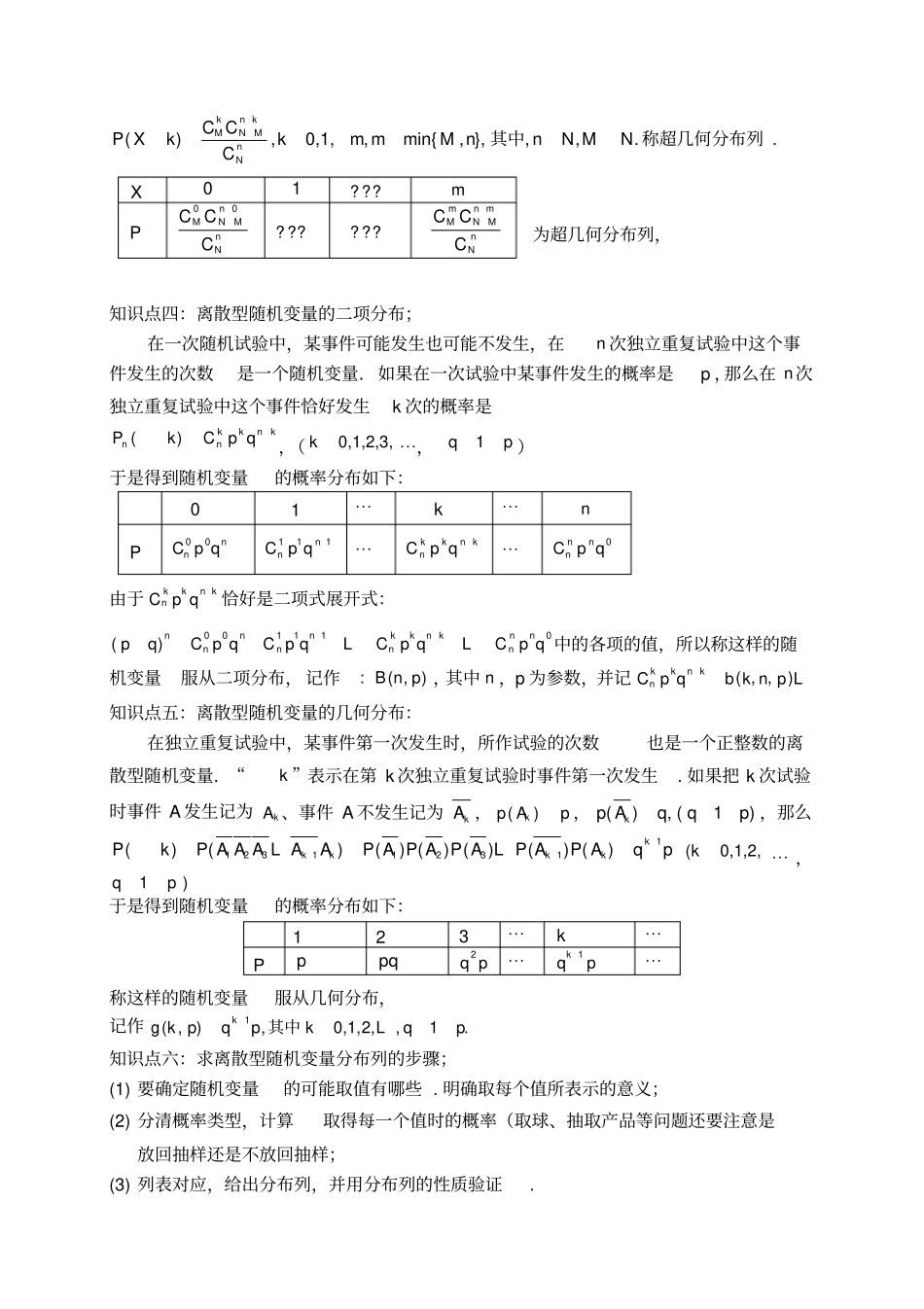
离散型随机变量及其分布知识点一:离散型随机变量的相关概念;随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量随机变量常用希腊字母、等表示离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。若是随机变量,ab ,其中 a 、 b 是常数,则也是随机变量连续型随机变量:对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定次序一一列出,而连续性随机变量的结果不可以一一列出离散型随机变量的分布列: 设离散型随机变量可能取的值为12ixxx、取每一个值1,2,ix i的概率为()iiPxp ,则称表1x2x⋯ix⋯P1p2p⋯ip⋯为随机变量的概率分布,简称的分布列知识点二:离散型随机变量分布列的两个性质;任何随机事件发生的概率都满足: 0( )1P A,并且不可能事件的概率为0 ,必然事件的概率为 1.由此你可以得出离散型随机变量的分布列都具有下面两个性质:(1) 01,2,ipi,;12(2) 1PPL特别提醒:对于离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率的和即1()()()kkkPxPxPxL知识点二:两点分布:若随机变量X 的分布列 : 则称 X的分布列为两点分布列 . 特别提醒: (1) 若随机变量 X 的分布列为两点分布 , 则称 X 服从两点分布 , 而称 P(X=1)为成功率 . (2)两点分布又称为 0-1 分布或伯努利分布 (3)两点分布列的应用十分广泛, 如抽取的彩票是否中奖; 买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等等;都可以用两点分布列来研究 . 知识点三:超几何分布:一般地,在含有 M 件次品的 N 件产品中,任取 n 件,其中恰有 X 件次品,则X0 1 P1PP(),0,1,,min{, },,,.kn kMNMnNC CP Xkkm mM nnN MNC其中称超几何分布列 . 为超几何分布列,知识点四:离散型随机变量的二项分布;在一次随机试验中,某事件可能发生也可能不发生,在n 次独立重复试验中这个事件发生的次数是一个随机变量.如果在一次试验中某事件发生的概率是p ,那么在 n次独立重复试验中这个事件恰好发生k 次的概率是knkknnqpCkP)(,(0,1,2,3,k⋯,pq1)于是得到随机变量的概率分布如下:01⋯k⋯nPnnqpC00111nnqpC⋯knkknqpC⋯0qpCnnn...