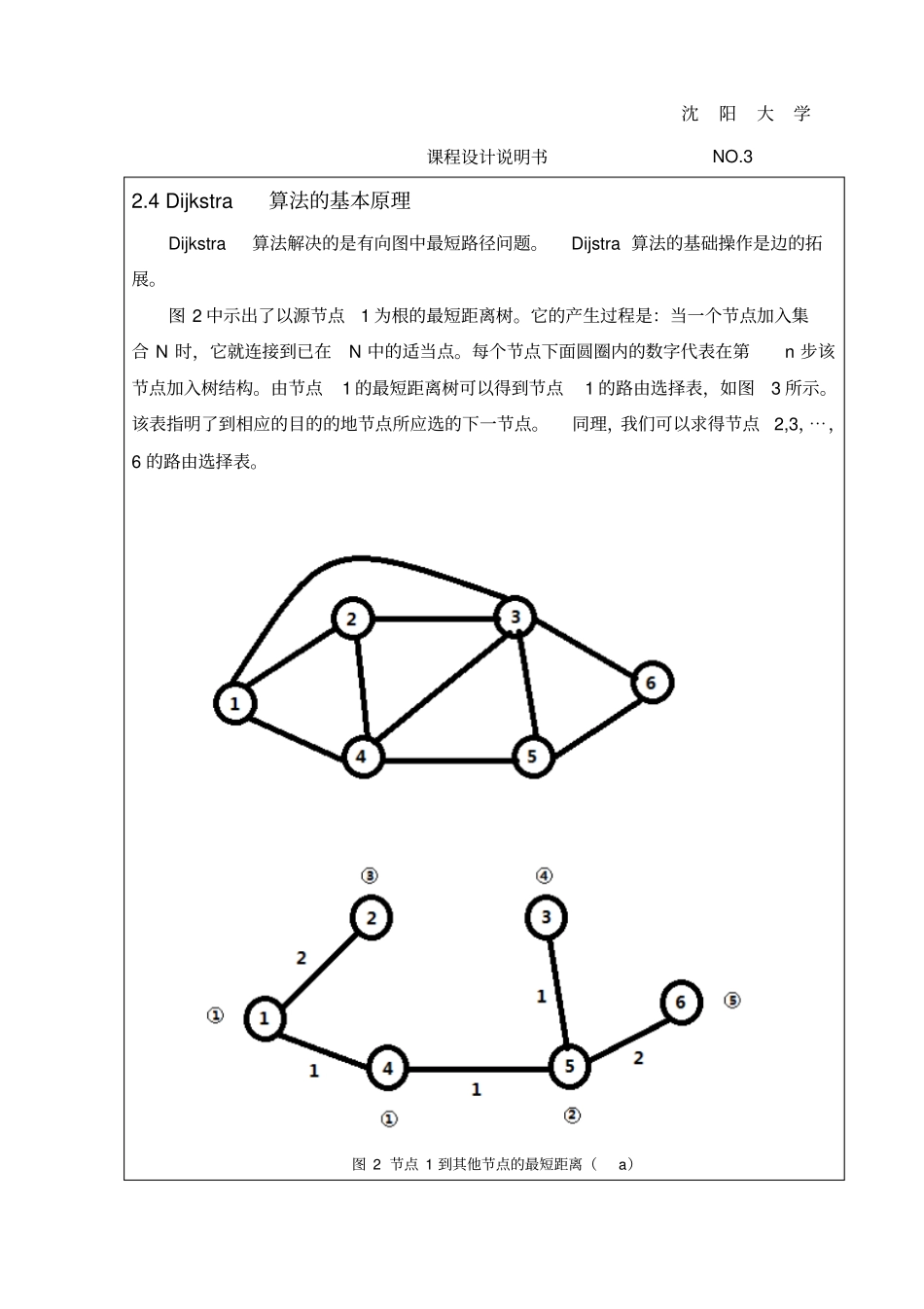
课程设计说明书 NO.1 C语言环境下 D算法完成最短路径求解1. 课程设计的目的为了巩固“通信网基础及应用”课程学到的相关知识,通过对本课程所学知识的综合运用,使学生融会贯通课程中所学的理论知识,初步掌握通信网络的体系结构和扩频通信系统等相关知识;加深对通信网络的基本理论、基本知识和常用技术的理解;提高学生分析问题的能力和实践能力,培养科学研究的独立工作能力。2. 设计方案论证2.1 最短路径算法的分类用于解决最短路径问题的算法被称做“最短路径算法”,有时被简称作“路径算法”。最常用的路径算法有:1.Dijkstra算法 , 是解决一个节点到其他节点之间的最短路径的问题。2.A* 算法。3.SPFA 算法。4.Bellman-Ford算法。5.Floyd-Warshall算法,可以用来求解网中任意两个节点之间的最短路径。6.Johnson算法。所谓单源最短路径问题是指:已知G=( V, E),我们希望找出从某给定的源结点 S∈V 到 V 中的每个结点的最短路径。首先,我们可以发现有这样一个事实:如果P是 G中从 vs 到 vj 的最短路, vi 是 P中的一个点,那么,从vs 沿 P到 vi 的路是从 vs 到 vi 的最短路。2.2 经典 Dijkstra算法的主要思想Dijkstra算法的基本思路是:假设每个点都有一对标号 (dj , pj) ,其中 dj 是从起源点 s 到点 j 的最短路径的长度 ( 从顶点到其本身的最短路径是零路( 没有弧的路 ) ,其长度等于零 ) ;pj 则是从 s 到 j 的最短路径中 j 点的前一点。 求解从起源点 s 到点 j 的最沈阳大学课程设计说明书 NO2 短路径算法的基本过程如下:第一步:初始化。令N={1} 。对于不在 N 中的每个节点 v,设置 D(v)=l(1,v)(对于与 1 不直接相连的节点取为∞)。第二步:找到一个不在N 中的使 D(w)最小的节点 w,并将 w 加进集 N 中去,然后计算下式,以修改不在N 中的所有其他节点的D(v):D(v)=min[D (v),D(w)+l(w,v)] 重复第二步,直至全部节点包括在N 中。2.3 Dijkstra算法的实现我们利用图 1 中所示的网作为例子讨论Dijkstra算法,我们的目的是求出源节点到网中所有其他节点的最短路径。在求解过程中,采取步进方式,建立一个以源节点1 为根的最短路径树,直到包括最远的节点在内为止。到第k 步,计算出到离源节点最近的k 个节点的最短路径。这些路径定义为在集 N内。图 1 一个网络的例子在按标记法实现Dijkstra算法的过程中,核心步...