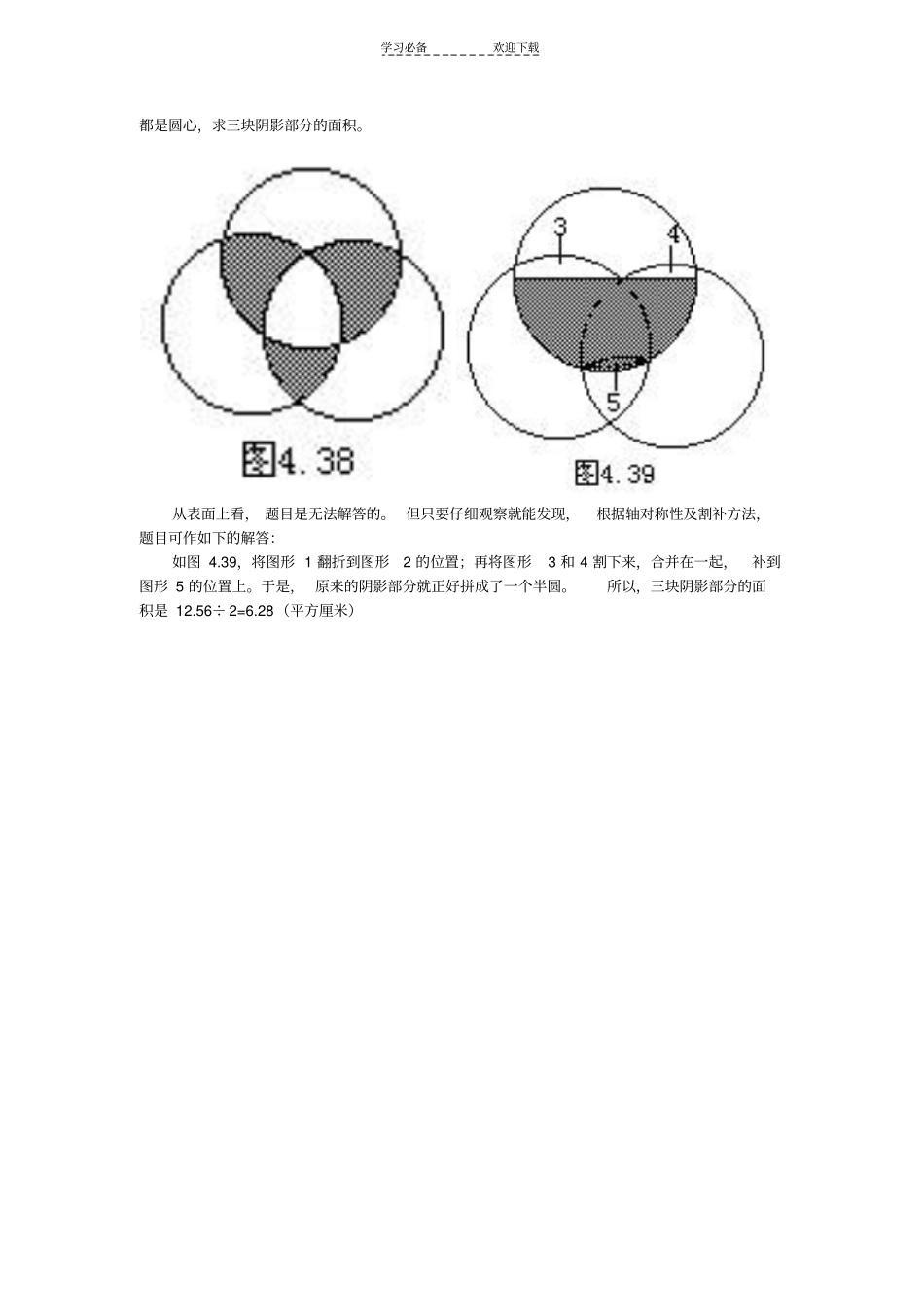
学习必备欢迎下载解题技巧1.等分图形【均分整体】 有些几何问题, 只要把大图形均分为若干个小图形,就能找到问题的答案。例如,下面两图中的正方形分别内接于同一个等腰直角三角形(内接指四个顶点全在三角形的边上) 。已知左图(图4.11)中正方形面积为72 平方厘米,求右图(4.12)中正方形的面积。由于左右两个三角形完全相同,我们不妨把这两个图形进行等分,看看这两个正方形分别与同一个等腰直角三角形有什么样的关系。等分后的情况见图4.13 和图 4.14。积是图 4.12 的正方形面积是2.【平移空白或阴影部分】有些求阴影部分或空白部分面积的几何题,采用平移空白部分或平移阴影部分的办法,往往能化难为易,很快使问题求得解答。例如,计算图4.20 中阴影部分的面积。学习必备欢迎下载圆面积”,然后相加,得整个阴影部分的面积。这显然是很费时费力的。但认真观察一下就会发现,图4.20 左半左上部的空白部分,与右半左上部的阴影部分大小一样,只需将右半左上部的阴影部分, 平移到左半左上部的空白部分,所有的阴影部分便构成一个正方形了(如图 4.21)。所以,阴影部分的面积很快就可求得为5×5=25。3.【旋转成定角】例如下面的题目:又如,如图4.25,求正方形内阴影部分的面积。(单位:厘米)表面上看,题目也是很难解答的。但只要将两个卵叶片形的阴影部分绕正方形的中心,分别按顺时针和逆时针方向旋转90° ,就得到了一个由阴影部分组成的半圆(如图4.26),于是,阴影部分的面积就很容易解答出来了。(解答略)【开扇式旋转】 有些图形相互交错,增加了解答的难度。若像打开折扇一样,绕着某个定点作“开扇式”旋转,往往会使人顿开茅塞,使问题很快获得解决。例如,求图4.27 的阴影部分的面积(单位:厘米)。若采用正方形面积减空白部分面积的求法,计算量是很大的。 由于它是由两个形状相同的扇形交叉重叠而成的,我们不妨把右下部的扇形打开,顺时针方向旋转90° ,得到图 4.28;再继续旋转,得到图4.29。在图 4.29 中,阴影部分面积便是半圆面积减三角形面积的差。所以,阴影部分面积是42×3.14÷2-(4+4)× 4×2 =25.12-16 =9.12(平方厘米)4.【割补】 在数学中, 把图形的某个部分割下,补到某一个新的位置,往往可以使新的图形,更便于发现数量关系,从而较快地解答出数学题目。例如, 在图 4.38 中,三个圆的面积都是12.56 平方厘米, 且三个圆两两相交,三个交点学习必备欢迎下载都是圆心...