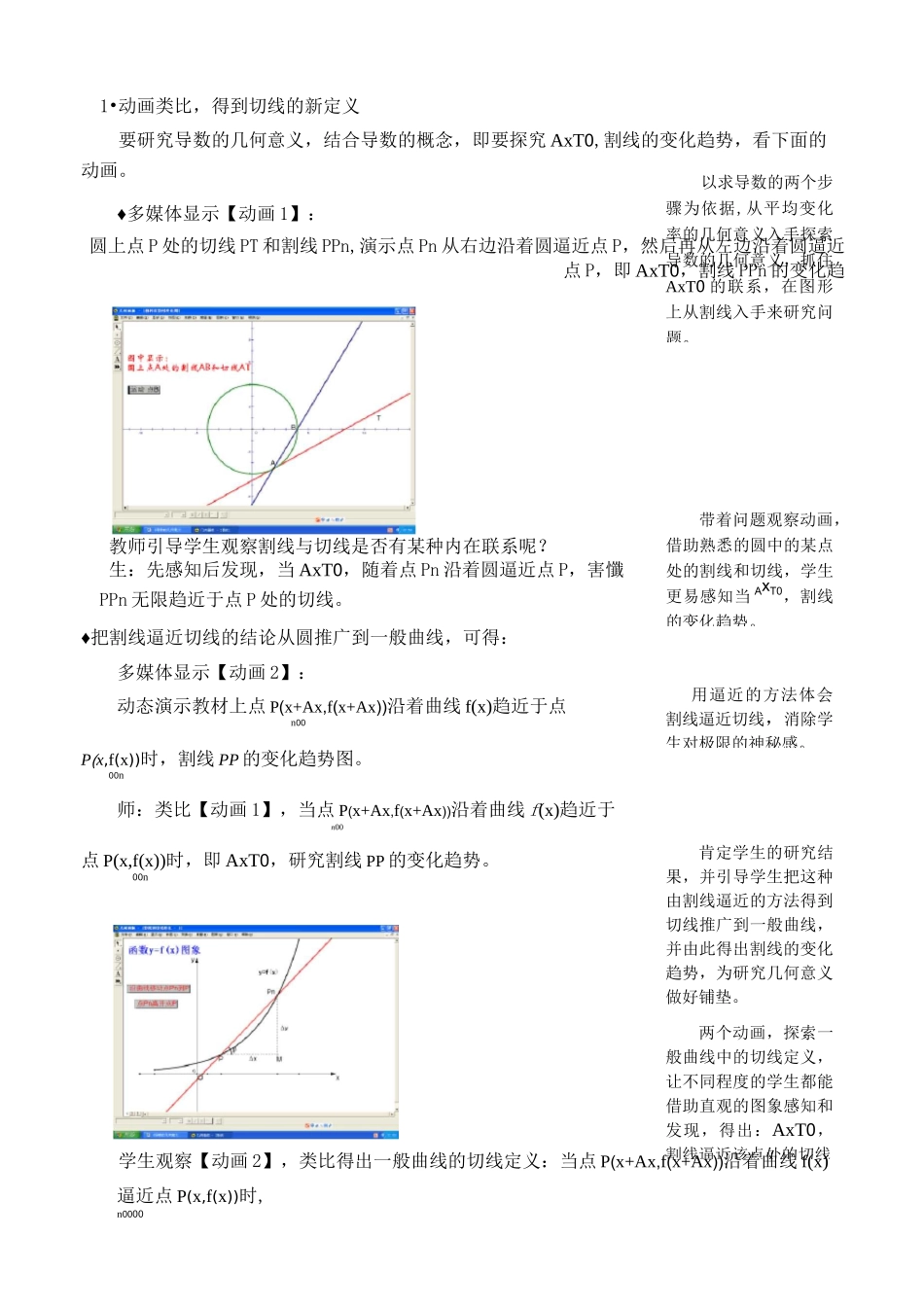
设计意图老师引导学生回忆联系本节课的旧知识,下面探究导数的几何意义也是依据导数概念的形成,寻求解决问题的途径。教师板书,便于学生数形结合探究导数的教学过程一、创设情境、导入新课1•回顾旧知、引出研究的问题:前面我们初步了解了一些微积分背景知识,对有“微积分之父”之称的牛顿和莱布尼慈,也相识了(幽默:同时知道当爹的不易),之后重点学习了函数在 x 二 x 处的导数广(x)就是函数在该点处的瞬时变化 00•・・・率。那么:提问:(1)求导数 f(x)的步骤有哪几步?0生:总共分三步(拉音,模仿赵本山):第一步:求增量 Ay第二步:求平均变化率 Ay=f(x° + 心 ) - f ( x ° );AxAx第三步:求瞬时变化率 f©)=limf(x° +A x ) - f ( x ° )•0AXTOAx(即 AxT0,平均变化率趋近于的确定常数就是该点导数)(2)观察函数 y 二/(x)的图象,平均变化率 Ay=f(x° + 心) - f ( x ° )AxAx在图形中表示什么突破平均变化率的几何意义,后面在表示割线斜率时能直接联系此知识。同时引出本节课的研究问题一一导数几何意义是什么?(复习引入用时约 3 分钟)生:平均变化率表示的是割线 PP 的斜率.n师:这就是平均变化率(型)的几何意义,那么瞬时变化率(limAy)Ax 心 TOAx在图中又表示什么呢?今天我们就来探究导数的几何意义。板书、引导探究、获得新知以求导数的两个步骤为依据,从平均变化率的几何意义入手探索导数的几何意义,抓住AxT0 的联系,在图形上从割线入手来研究问题。带着问题观察动画,借助熟悉的圆中的某点处的割线和切线,学生更易感知当 AxT0,割线的变化趋势。用逼近的方法体会割线逼近切线,消除学生对极限的神秘感。肯定学生的研究结果,并引导学生把这种由割线逼近的方法得到切线推广到一般曲线,并由此得出割线的变化趋势,为研究几何意义做好铺垫。两个动画,探索一般曲线中的切线定义,让不同程度的学生都能借助直观的图象感知和发现,得出:AxT0,割线逼近该点处的切线1•动画类比,得到切线的新定义要研究导数的几何意义,结合导数的概念,即要探究 AxT0,割线的变化趋势,看下面的动画。♦多媒体显示【动画 1】:圆上点 P 处的切线 PT 和割线 PPn,演示点 Pn 从右边沿着圆逼近点 P,然后再从左边沿着圆逼近点 P,即 AxT0,割线 PPn 的变化趋教师引导学生观察割线与切线是否有某种内在联系呢?生:先感知后发现,当 AxT0,随着...