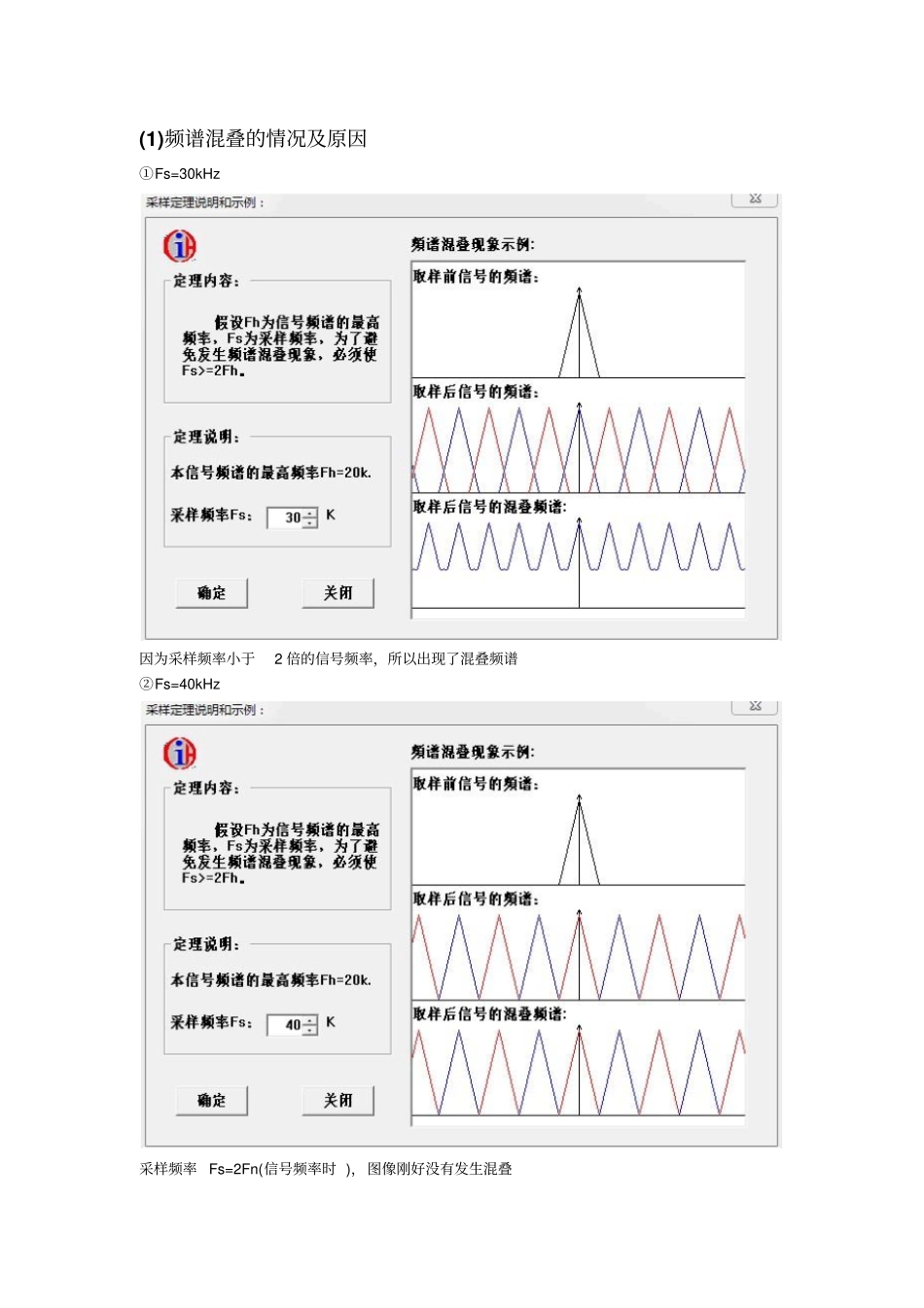
(1)频谱混叠的情况及原因①Fs=30kHz 因为采样频率小于2 倍的信号频率,所以出现了混叠频谱②Fs=40kHz 采样频率 Fs=2Fn(信号频率时 ),图像刚好没有发生混叠③Fs=60kHz 采样频率 Fs>2Fn(信号频率时 ),图像没有发生混叠结论: Fh 为信号频谱的最高频率,Fs 为采样频率,为了避免发生混叠,应该使Fs>=2Fh 。(2)四种信号的傅立叶变换关系①非周期连续信号-------> 非周期连续信号②周期连续信号-------> 非周期离散信号③非周期离散信号--------> 周期连续信号④周期离散信号--------> 周期离散信号结论:连续非周期信号的傅里叶变换为连续非周期的;连续周期信号的傅里叶变换为离散的;离散信号的傅里叶变换为连续周期的;离散周期信号的傅里叶变换为离散周期的。(3)信号泄漏①因为 N=16 ,Fn=0.2SF/2,所以信号的频率介于1* △f 与 2* △f 之间,导致 FFT 分析的结果将该信号的频率成分泄漏到它的周围的一些离散的频率点上②因为 N=16 ,Fn=0.5SF/2,所以信号的频率为4* △f 上, FFT 能准确分析该信号的频率点上的幅值结论:如果信号采样频率为SF Hz ,信号的分析点数为N,则 FFT 分析结果的频率分辨率为Δ f=SF/N, 当信号的频率恰好为k* Δ f 时( k=0,1,2 ⋯⋯ N/2)没有泄漏,当频率在k* Δ f到( k+1)*f 之间,则有泄漏。(4)信号混叠:①当两个通道的信号都小于SF/2=2000Hz 时:②一通道的信号大于SF/2=2000Hz 的部分开始出现混叠: ③一通道的信号大于SF/2=2000Hz 的部分即会出现混叠的图像:结论:采样时,如果信号频率f> 采样频率SF 的一半时,采样后的信号就表现为一个低于SF/2 的频率成分, 产生不容易发现的错误,这就是信号混叠,为了避免除去大于SF/2 的成分,在采样前一般对信号进行0--SF/2的低通滤波。(5)连续有限信号取样①取样频率Fs=5Hz 时周期 T 为 20s,即信号的频率为0.05Hz ,此时的抽样频率为5Hz,满足了采样定理②取样频率Fs=0.5Hz 时周期 T 为 20s,即信号的频率为0.05Hz ,此时的抽样频率为0.5Hz,满足了采样定理。结论:当周期T 一定时,抽样频率越大,其采样的时间间隔越短,图像越逼真(6)连续无限信号取样①取样角频率为2W0 时:信号的频率为W0=2π /T,并且抽样频率为Ws=2w0,处于采样混叠的临界状态,但是由于K=2 与-2 及其整数倍时,信号有值,所以导致采样后的图像失真。②取样角频率为8W0 时:信号的频率为W0=2π /T,并且抽...