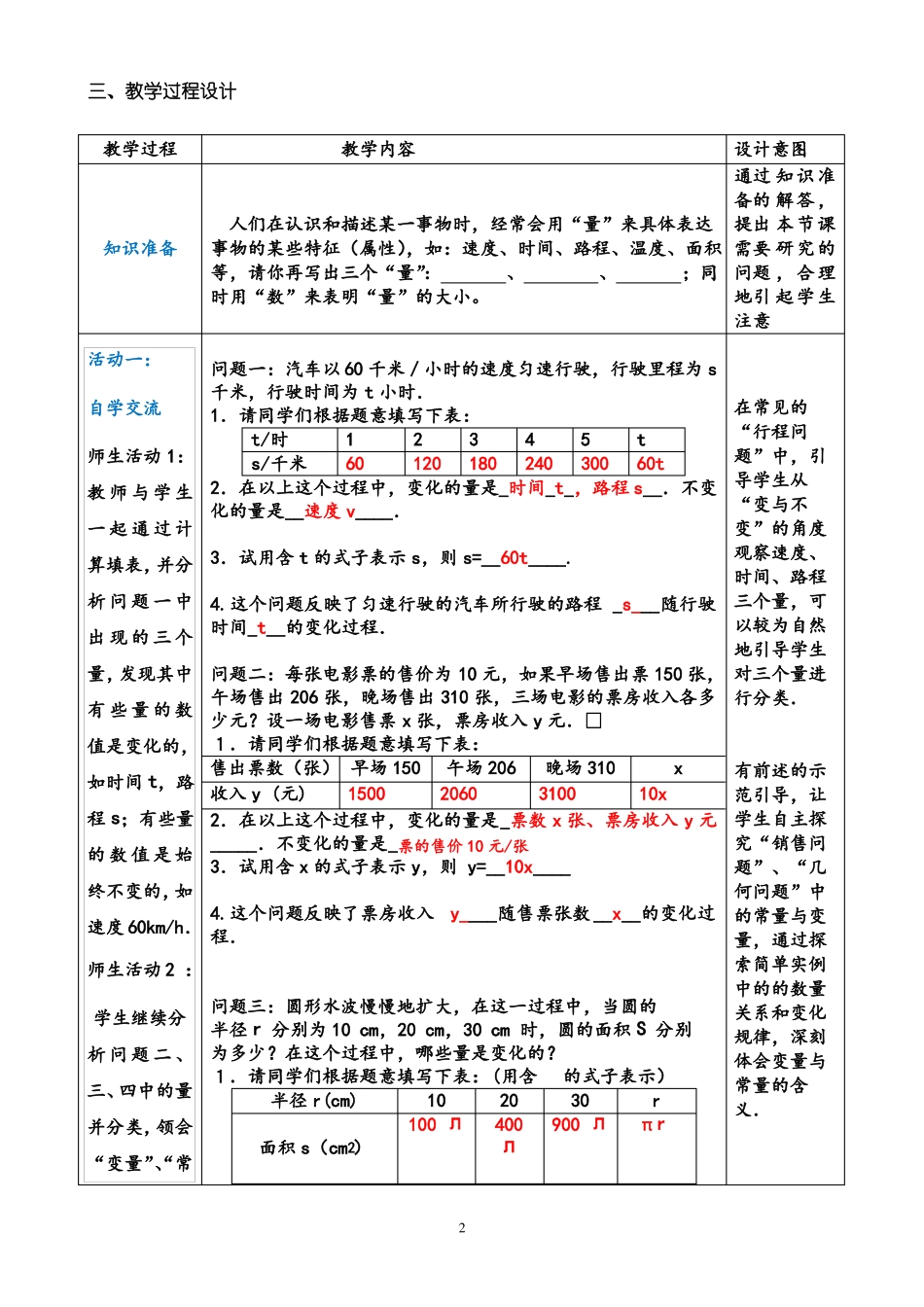
19.1.1《变量与函数》(第1课时)教学设计一、教材内容和内容分析内容内容本课是函数的起始课,函数是刻画运动变化现象的重要数学模型,要从数学的角变量与常量的概念分析度研究变化现象,把握变化规律,首先要关注变化过程中量的变化,这就是变量.有了变量的概念,便为研究成函数关系的两变量的“运动与对应”关系打下基础.本课从四个简单的实际问题入手,通过分析问题中数值的变与不变,引出变量与常量的概念,而且问题中变量的单值对应关系也为学习函数的定义作了铺垫.基于以上分析,确定本节课的教学重点是:能找出一个变化过程中的变量与常量,了解常量与变量的意义.变量是学生第一次接触,对一个运动变化过程中的两个变量的关系,学生往往只认为是一种确定的数量关系,类似于二元一次方程,没有用运动与变化的观点去体会两个变量之间相互依赖的变化.基于以上分析,确定本节课的教学难点为:体会运动变化过程中量的变化,较复杂问题中常量与变量的识别.二、教学目标和重难点知识技能结合丰富的实例,让学生在具体的情景中领悟常量与变量的含义,能分清实例中的常量与变量,在具体教学中培养学生的数学阅读能力.教学目标数学思考通过感受运动与变化的数量关系初步体验函数思想.解决问题通过阅读课本知识,抓住关键词,感受常量与变量的意义.情感态度感受变量是刻画现实生活中许多变化事物的一种重要的数学工具,加深学生对数学来源于生活的体验。重点能找出一个变化过程中的变量与常量,了解常量与变量的意义.难点体会运动变化过程中量的变化,较复杂问题中常量与变量的识别.1三、教学过程设计教学过程设计意图通过 知识准备的 解答,人们在认识和描述某一事物时,经常会用“量”来具体表达提出 本节课事物的某些特征(属性),如:速度、时间、路程、温度、面积 需要 研究的等,请你再写出三个“量”:、、;同问题 ,合理地引 起学生时用“数”来表明“量”的大小。注意问题一:汽车以 60 千米/小时的速度匀速行驶,行驶里程为 s千米,行驶时间为 t 小时.在常见的1.请同学们根据题意填写下表:“行程问t/时12345t题”中,引s/千米6012018024030060t2.在以上这个过程中,变化的量是_时间_t_,路程 s__.不变导学生从“变与不化的量是__速度 v____.变”的角度观察速度、3.试用含 t 的式子表示 s,则 s=__60t____.时间、路程4.这个问题反映了匀速行驶的汽车所行驶的路程 _s___随行驶三个量,可以较为自然时间_t__...