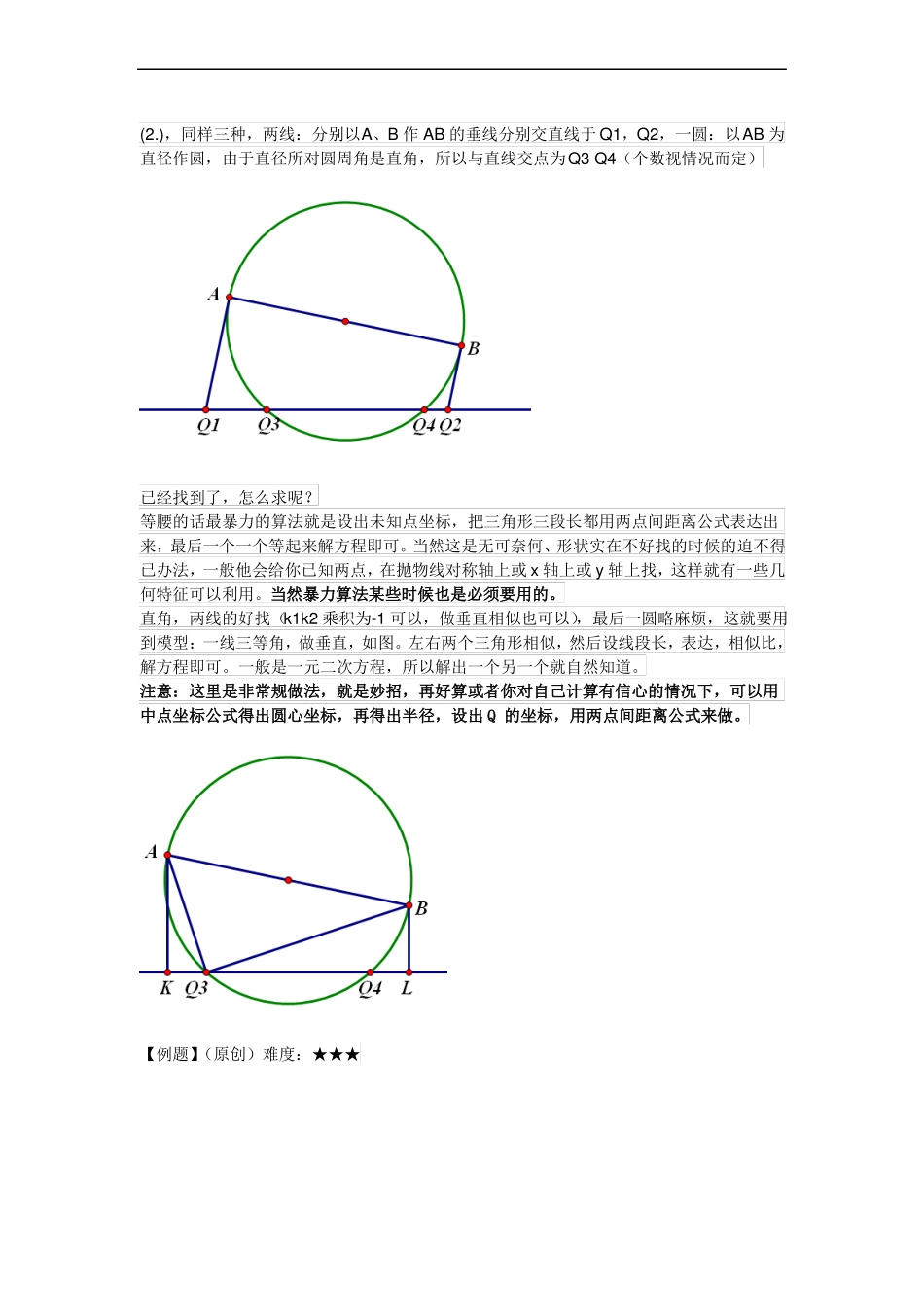
【坐标系压轴专题】坐标系中的问题，一般出在压轴题，不是压轴题也会有很大的难度，针对此便有了这个专题【1】坐标系问题的基本运算实用度：★★★★如果想要熟练地解坐标系中的问题，先掌握下列的几个重要点（看不清放大看）前三点、最后一点稍难，有口诀：两点间距离公式：横坐标相减的平方加纵坐标相减的平方开根号斜率 k：竖直高度比水平宽度中点坐标公式：横坐标的平均数，纵坐标的平均数平移函数图像：左增右减，上加下减【例题 1】（原创）难度：★★★★答案：【2】等腰三角形、直角三角形存在性基础做起，实用性：★★★关键词：等腰两圆一线，直角两线一圆这两点放在一起是为了对比，它们都需要分类讨论
什么叫做两圆一线、两线一圆呢
举个例子，如图，AB 线段一条，在下面那根直线上找 P 和 Q，使得(1
)△ABP 是等腰三角形 (2
)△ABQ 是直角三角形首先(1
)，有三种可能（AB=AP，AB=BP，AP=BP），两圆：以A 为圆心，AB 为半径画圆，与直线交于 P1，还有一个圆是以 B 为圆心，AB 为半径画圆与直线交于 P2 和 P3
最后一线：AB 的垂直平分线与直线交于 P4，P5（有时不一定 5 个，视情况而定）(2
)，同样三种，两线：分别以A、B 作 AB 的垂线分别交直线于 Q1，Q2，一圆：以AB 为直径作圆，由于直径所对圆周角是直角，所以与直线交点为Q3 Q4（个数视情况而定）已经找到了，怎么求呢
等腰的话最暴力的算法就是设出未知点坐标，把三角形三段长都用两点间距离公式表达出来，最后一个一个等起来解方程即可
当然这是无可奈何、形状实在不好找的时候的迫不得已办法，一般他会给你已知两点，在抛物线对称轴上或 x 轴上或 y 轴上找，这样就有一些几何特征可以利用
当然暴力算法某些时候也是必须要用的
直角，两线的好找（k1k2 乘积为-1 可以，做垂直相似也可以），最后一圆略麻烦，这就要
