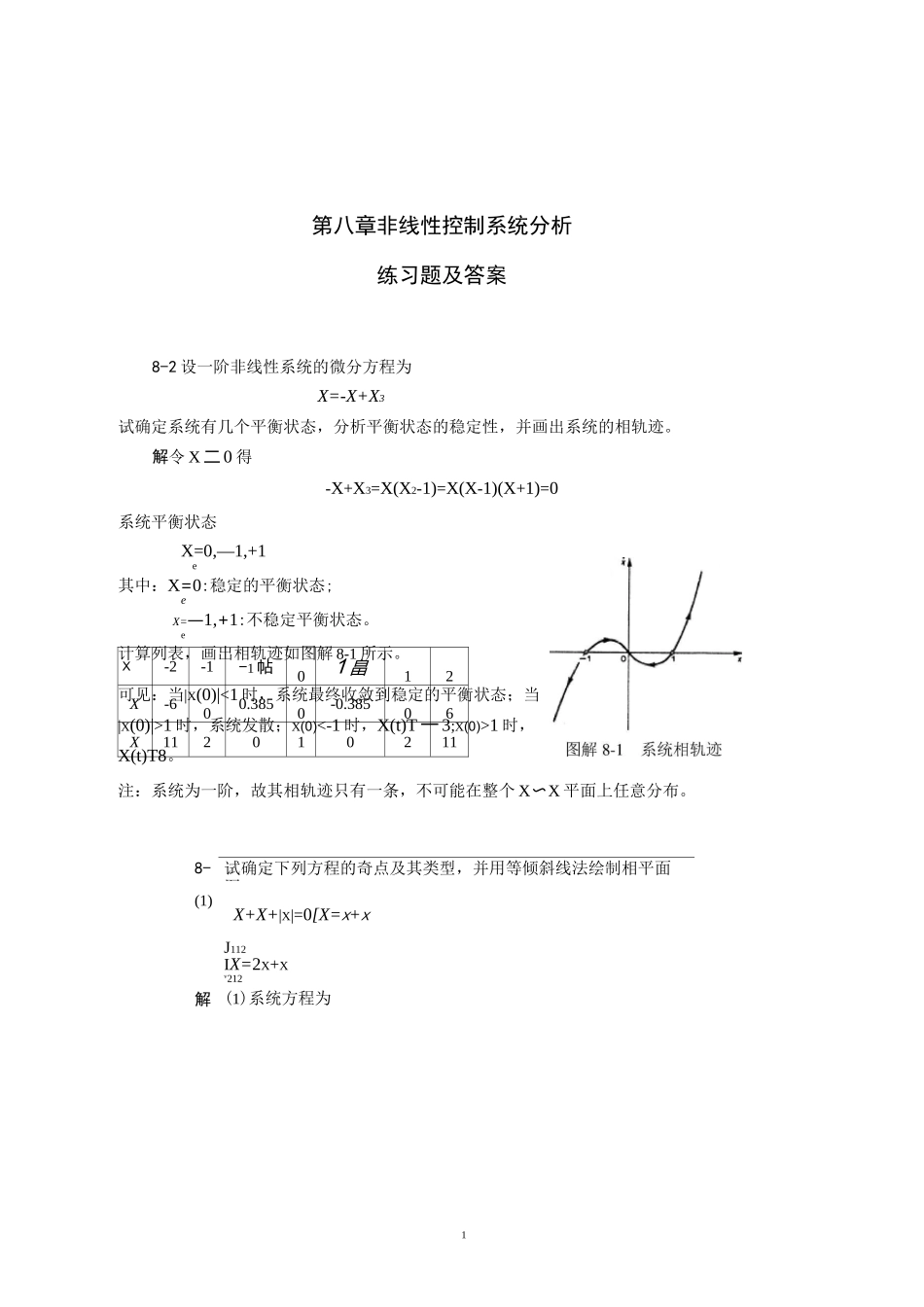
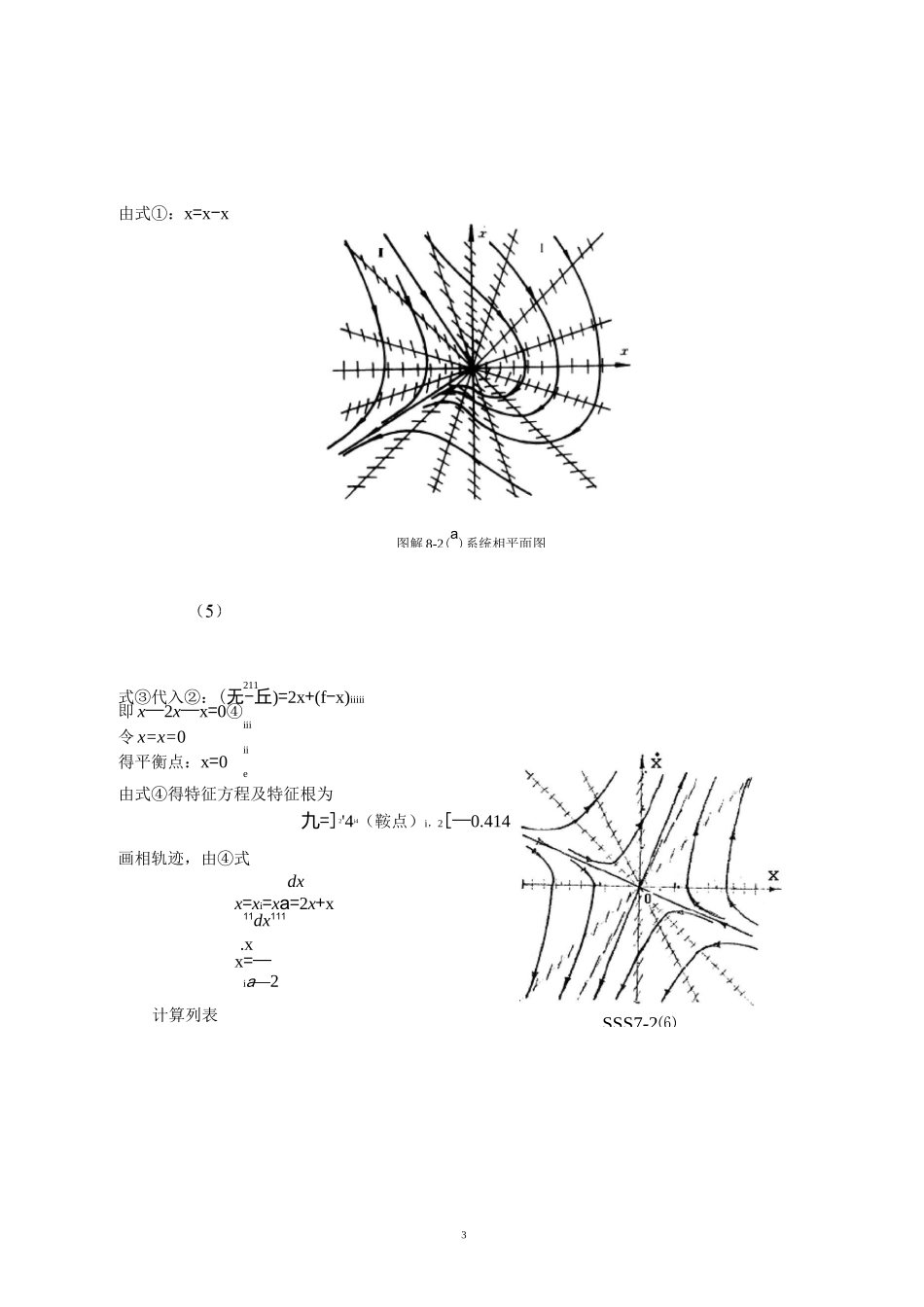
1X-2-1-1 帖01 畠12X-600.3850-0.38506X112010211第八章非线性控制系统分析练习题及答案8-2 设一阶非线性系统的微分方程为X=-X+X3试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。解令 X 二 0 得-X+X3=X(X2-1)=X(X-1)(X+1)=0系统平衡状态X=0,—1,+1e其中:X=0:稳定的平衡状态;eX=—1,+1:不稳定平衡状态。e计算列表,画出相轨迹如图解 8-1 所示。可见:当|X(0)|<1 时,系统最终收敛到稳定的平衡状态;当|X(0)|>1 时,系统发散;X(0)<-1 时,X(t)T 一 3;X(0)>1 时,X(t)T8。注:系统为一阶,故其相轨迹只有一条,不可能在整个 X〜X 平面上任意分布。8-3试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。(1)X+X+|X|=0[X=X+XJ112IX=2X+Xv212解 (1)系统方程为2II:s2+s-1=0,s1,2=-1.618,+0.618(鞍I:x+x+x=0(x>0)H:x+x-x=0(x<0)令 x=x=0,得平衡点:x=0。e系统特征方程及特征根:1:s2+s+1=0,S1,2=-2 士哙(稳定的焦点)dx.x=-x-xdxa=竺=-1-扯dxxI:2=-1-|(x>0)II:2=|-1(x<0)计算列表.8-3-1-1/301/313OOx>0:2=-1—1B-1-2/302-8-4-2-4/3-1x<0:2=-1+1/P-1-4/3-2-4OO20-2/3-1用等倾斜线法绘制系统相平面图如图解 8-2(a)所示。3由式①:x=x-x211式③代入②:(无-丘)=2x+(f-x)iiiii即 x—2x—x=0④iii令 x=x=0ii得平衡点:x=0e由式④得特征方程及特征根为九=]2'4i4(鞍点)i,2[—0.414画相轨迹,由④式dxx=xi=xa=2x+x11dx111.xx=—ia—2计算列表图解 8-2(a)系统相平面图SSS7-2⑹40=(—1-2x)|x=X=0X-0.5X+x=0s1,=0.5 土'0.52-4=0.25 土 j0.984不稳定的焦点)x=-1特征s1,2=0.5 土牛<0.52+4=J1.218-0.718鞍点)a22.53OO11.52卩=1/(a-2)OO210-1-2OO用等倾斜线法绘制系统相平面图如图解 8-2(b)所示。8-4 若非线性系统的微分方程为(1)X+(3X-0.5)X+x+x2=0(2)X+xX+x=0 试求系统的奇点,并概略绘制奇点附近的相轨迹图。解(1)由原方程得X=f(x,X)=-(3X-0.5)X-x-x2=一 3X2+0.5X-x-x2令X=X=011得X+X2=X(X+1)=0解出奇点X=0,-1e在奇点处线性化处理。在 x=0 处:e坊(x,X)-xdX.xuxX=0丘=0•x+(-6X+0.5)-X=-x+0.5Xx=X=0特征方程及特征根=—1 处X=(-1—2x)-x+(-6X+0.5)-X=x+0.5XX=-1X=0X-0.5X-x=0概略画出奇点附近的相轨迹如图解 8-4(1)所示:+-••丿x=东•x+fdX由综合点0|e|<2Im(t)=2He(t)+2e<—2皿5=—xX—x二 0,在奇点处线性化x=X=0=(—X—1)•x—xx=X=0特征根 S=±j。奇点 x=0(中心点)处...