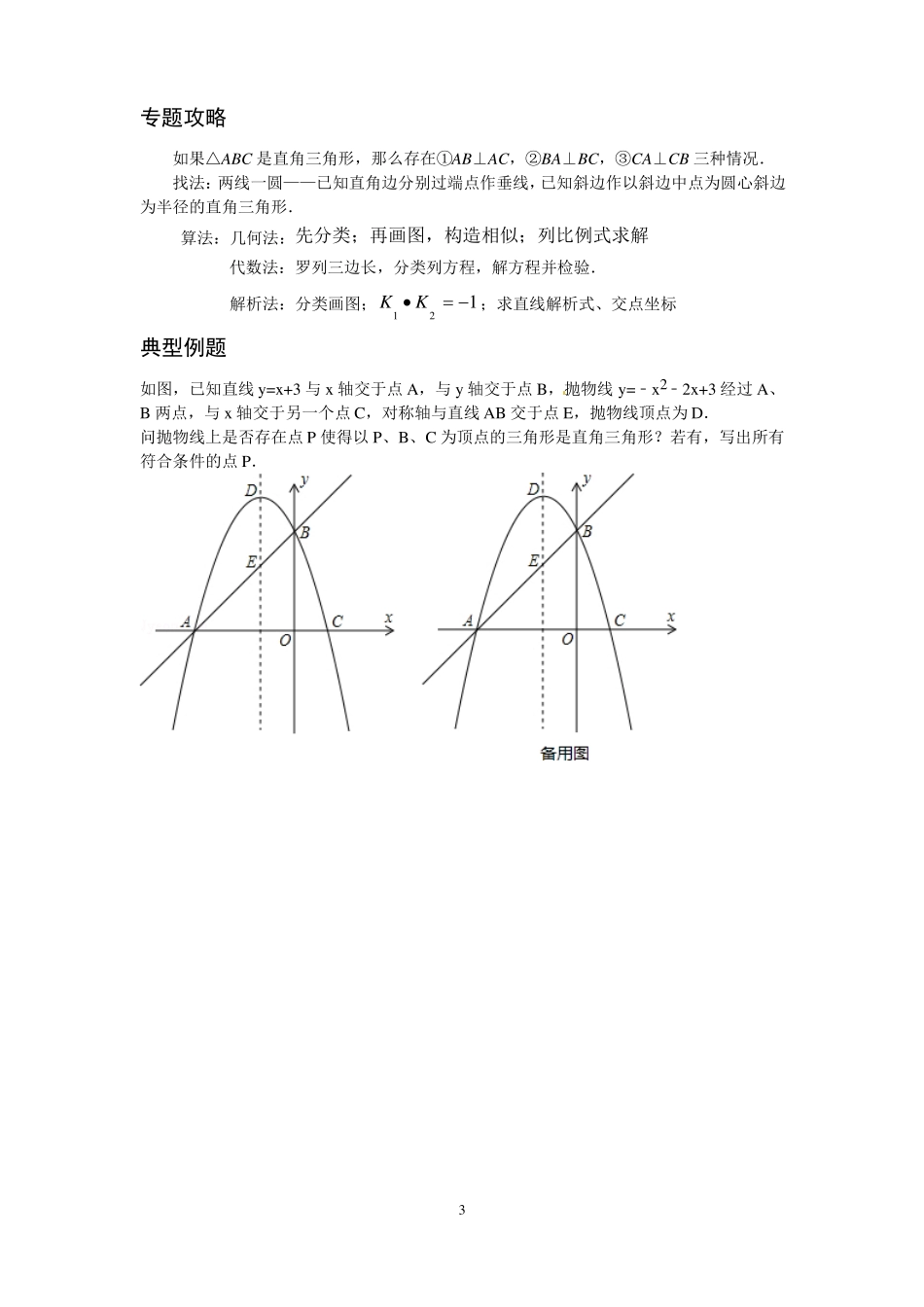
专题训练二等腰三角形、直角三角形的存在性问题专题攻略如果△ABC 是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB 三种情况.找法:两圆一线——已知腰长分别作以端点为圆心腰长为半径的圆,已知底边作底边的垂直平分线.算法:几何法:分类、画图、计算.代数法:罗列三边长,分类列方程,解方程并检验.典型例题如图,已知直线 y=x+3 与 x 轴交于点 A,与 y 轴交于点 B,抛物线 y=﹣x ﹣2x+3 经过 A、B 两点,与 x 轴交于另一个点 C,对称轴与直线 AB 交于点 E,抛物线顶点为 D.问 x 轴上是否存在点 P 使得以 P、B、C 为顶点的三角形是等腰三角形?若有,写出所有符合条件的点 P.21变式:问 y 轴正半轴上是否存在点 P 使得以 P、B、C 为顶点的三角形是以 BC 为腰的等腰三角形?若有,写出所有符合条件的点 P.2专题攻略如果△ABC 是直角三角形,那么存在①AB⊥AC,②BA⊥BC,③CA⊥CB 三种情况.找法:两线一圆——已知直角边分别过端点作垂线,已知斜边作以斜边中点为圆心斜边为半径的直角三角形.算法:几何法:先分类;再画图,构造相似;列比例式求解代数法:罗列三边长,分类列方程,解方程并检验.解析法:分类画图;K1 K2 1;求直线解析式、交点坐标典型例题如图,已知直线 y=x+3 与 x 轴交于点 A,与 y 轴交于点 B,抛物线 y=﹣x ﹣2x+3 经过 A、B 两点,与 x 轴交于另一个点 C,对称轴与直线 AB 交于点 E,抛物线顶点为 D.问抛物线上是否存在点 P 使得以 P、B、C 为顶点的三角形是直角三角形?若有,写出所有符合条件的点 P.23变式:(1)问对称轴上是否存在点 P 使得以 P、B、C 为顶点的三角形是 BC 为斜边的直角三角形?若有,写出所有符合条件的点 P.4练习1.如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点 O.P 为二次函数图象上的一个动点,过点 P 作 x 轴的垂线,垂足为 D(m,0),并与直线 OA 交于点 C.(1)求出二次函数的解析式;(2)当点 P 在直线 OA 的上方时,用含 m 的代数式表示线段 PC 的长,并求线段 PC 的最大值;(3)当 m>0 时,探索是否存在点 P,使得△PCO 为等腰三角形,如果存在,请直接写出所有 P 的坐标;如果不存在,请说明理由.52. 如图,在平面直角坐标系 xoy 中,矩形 ABCD 的边 AB 在 x 轴上,且 AB=3,BC=2 3 ,直线 y=3x 2 3经过...