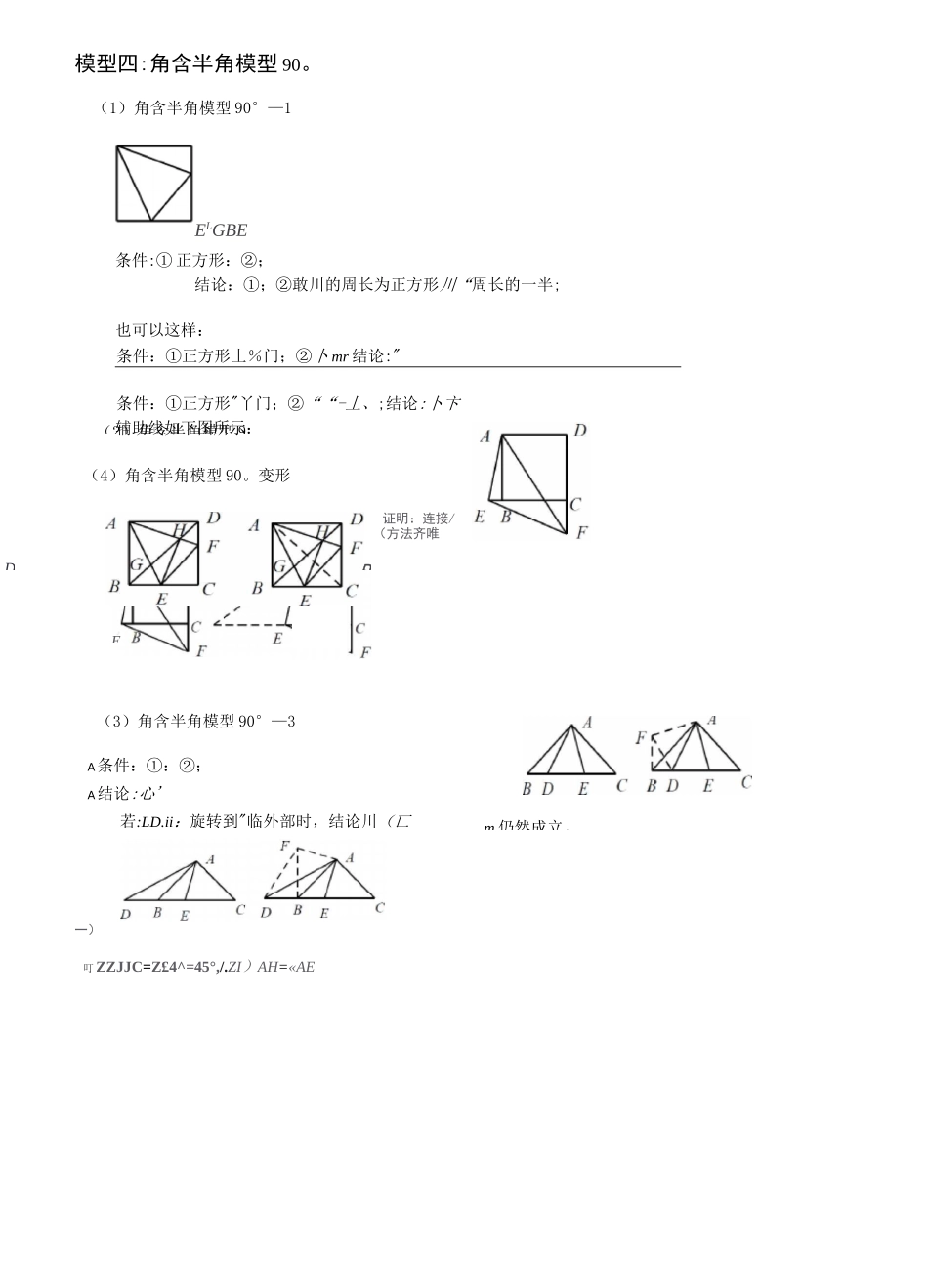
初中几何常见模型解析模型一:手拉手模型-旋转型全等(1)等边三角形A条件 f'im 均为等边三角形A结论:①:②;③门厂平分 G 口'(2)等腰用八A条件:弋 HX'im 均为等腰直角三角形A 结论:①:②厂匕A③ 平分ABAH(3)任意等腰三角形A 条件:“m 均为等腰三角形 A 结论:①:②,丄A③ 平分二打模型二:手拉手模型-旋转型相似(1)一般情况A 条件:{门弟,将讥"”旋转至右图位置 A 结论:A 右图中① K 入 D:■A② 延长 AC 交 BD 于点 E,必有 n'z皿口(2)特殊情况A 条件:{门'占,,将旋转至右图位置A 结论:右图中①;②延长 AC 交 BD 于点 E,必有“打(=八"八;BD0D③“一 M⑤连接 AD、BC,必有'1(}1/>>(-;「「";S4Hf.ty■—ACJxBD⑥"•二(对角线互相垂直的四边形)模型三:对角互补模型(1)全等型-90。A 条件:① n:—山 1;②°C 平分 rmA 结论:① CD=CE;②()n1(J/--、m;③^ODCE=十^ihOCE=亍皿A 证明提示:① 作垂直,如图,证明丸"叮二'(八;② 过点 C 作,如上图(右),证明;A 当的一边交 AO 的延长线于点 D 时:以上三个结论:①CD=CE(不变);②"厂皿—;③*.此结论证明方法与前一种情况一致,可自行尝试。(2)全等型-120。A 条件:①-120';A② 平分「If;A 结论:①:②宀、mf";③1证明提示:① 可参考“全等型-90°”证法一;② 如图:在 OB 上取一点 F,使 0F=OC,证明讥"为等边三角形。⑶ 全等型-任意角◎A 条件:①;:汗一\RM 厂一「7」_f-'-;②{门(>.;A 结论:①f"平分「if」劈:②;A③■\lliX•\:,1VA 当的一边交 AO 的延长线于点 D 时(如右上图):原结论变成:①②;③;可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。F>/?A 对角互补模型总结:①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线;②初始条件“角平分线”与“两边相等”的区别;③两种常见的辅助线作法;④注意平分时,一一二〔一二(相等如何推导?(2)角含半角模型 9(3)角含半角模型 90°—3A条件:①:②;A结论:心'若:LD.ii:旋转到"临外部时,结论川(匸m 仍然成立。模型四:角含半角模型 90。(1)角含半角模型 90°—1ELGBE条件:① 正方形:②;结论:①;②敢川的周长为正方形川“周长的一半;也可以这样:条件:①正方形丄%门;②卜 mr 结论:"条件:①正方形"丫门;②““-丄、;结论:卜卞辅助线如下图所示:(4)角含半角...