现代信号处理教程胡广书(清华)

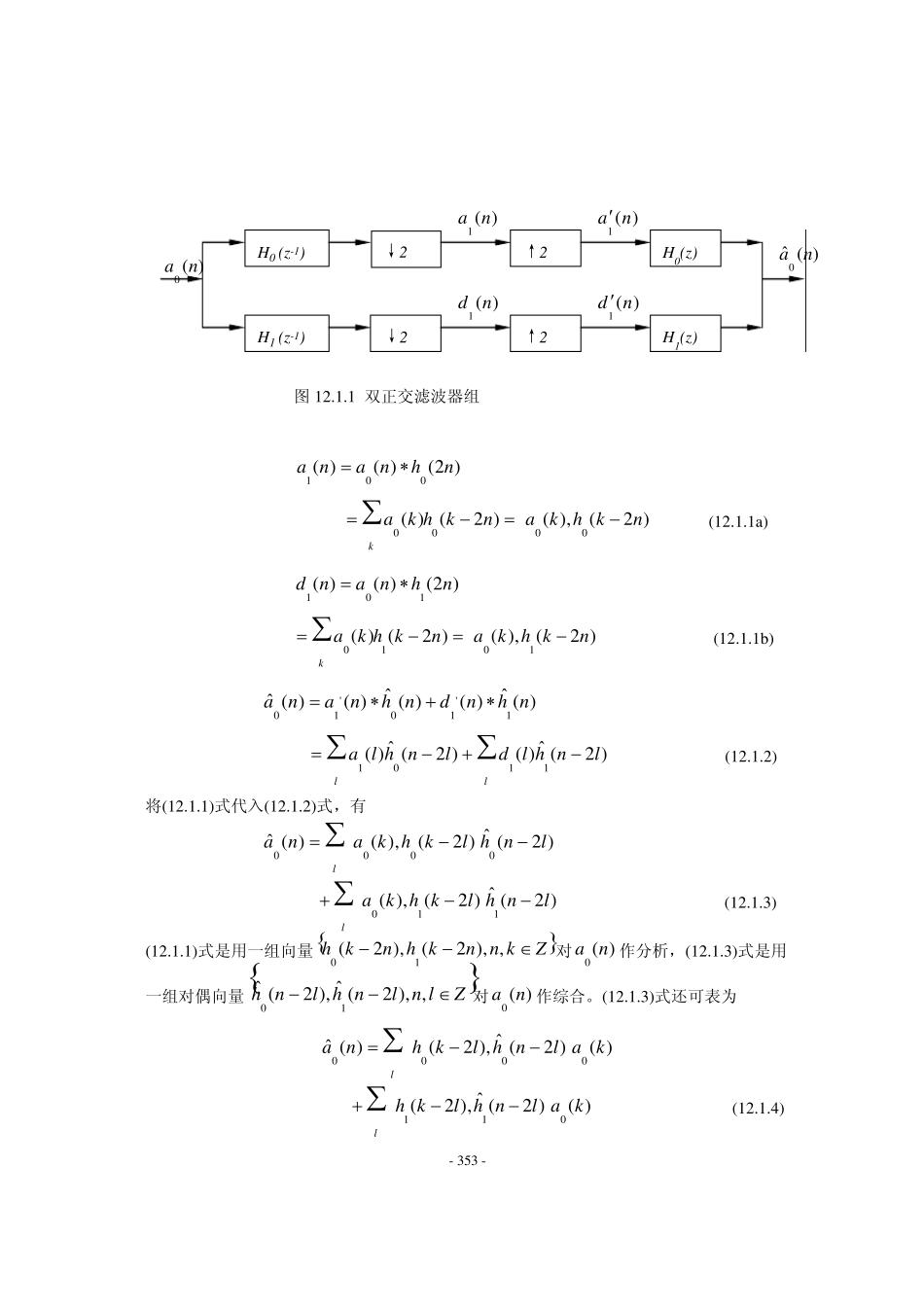
- 352 - 第 1 2 章 双正交小波及小波包 我们在上一章给出了正交小波的构造方法。正交小波有许多好的性质，如)()(),(',,'kkttkjkj ，)()(),(',,'kkttkjkj ，0)(),(',,ttkjkj ，此外，尺度函数和小波函数都是紧支撑的，有着高的消失矩等等。Daubechies 给出的正交小波的构造方法可以方便的构造出所需要的小波(如 DBN，SymN，CoifN)。但是，正交小波也有不足之处，即)(t和)(t都不是对称的，尽管 SymN 和 CoifN 接近于对称，但毕竟不是真正的对称，因此，这在实际的信号处理中将不可避免地带来相位失真。)(t和)(t的不对称性来自所使用的共轭正交滤波器组)(0 zH和)(1 zH的不对称性。我们已在 7.8 节讨论了具有线性相位的双正交滤波器组的基本概念，给出了可准确重建的双正交滤波器组的设计方法。本章，我们把这些内容引入到小波分析，给出适合小波变换的双正交滤波器组准确重建的条件，给出双正交条件下的多分辨率分析及双正交小波的构造方法，最后简要讨论小波包的基本概念 1 2 .1 双正交滤波器组 现在，我们结合小波变换的需要来研究双正交滤波器组的内在关系及实现准确重建的条件。所谓“小波变换的需要”是指在用)(0 zH对)(0 za分解时需要将)(0 zH和)(1 zH的系数作时间上的翻转，即用的是)(10zH及)(11zH，或)()(00nhnh,)()(11nhnh，见(10.6.1)式及图 10.6.2。将图 10.6.2 的正变换和图 10.6.3 的反变换结合起来，我们可得到如图 12.1.1 所示的一级分解和重建的类似于两通道滤波器组的信号流图。注意，图中用于重建的滤波器不再是图 10.6.3 中的)(0 zH和)(1 zH，而是)(ˆ0 zH和)(ˆ1 zH，它们分别是)(0 zH和)(1 zH的对偶滤波器。有关“对偶”的概念见 1.6 节，在下面的讨论中将涉及对偶滤波器的作用。 现在我们来分析该图中各信号之间的关系及实现PR 的条件。由第七章关于两通道滤波器组的理论，我们有 - 353 - 图12.1.1 双正交滤波器组 )2()()(001nhnana )2(),()2()(0000nkhkankhkak  (12.1.1a) )2()()(101nhnand )2(),()2()(1010nkhkankhkak  (12.1.1b) )(ˆ)()(ˆ)()(ˆ1'10'10nhndnhnana lllnhldlnhla)2(ˆ)()2(ˆ)(1101 (12.1.2) 将(12.1.1)式代入(12.1.2)式，有 )2(ˆ)2(),()(ˆ0000lnhlkhkanal  )2(ˆ)2(),(110lnhlkhkal (12.1.3) (12.1.1)式是用一...