第三章时域分析法作业与习题解答

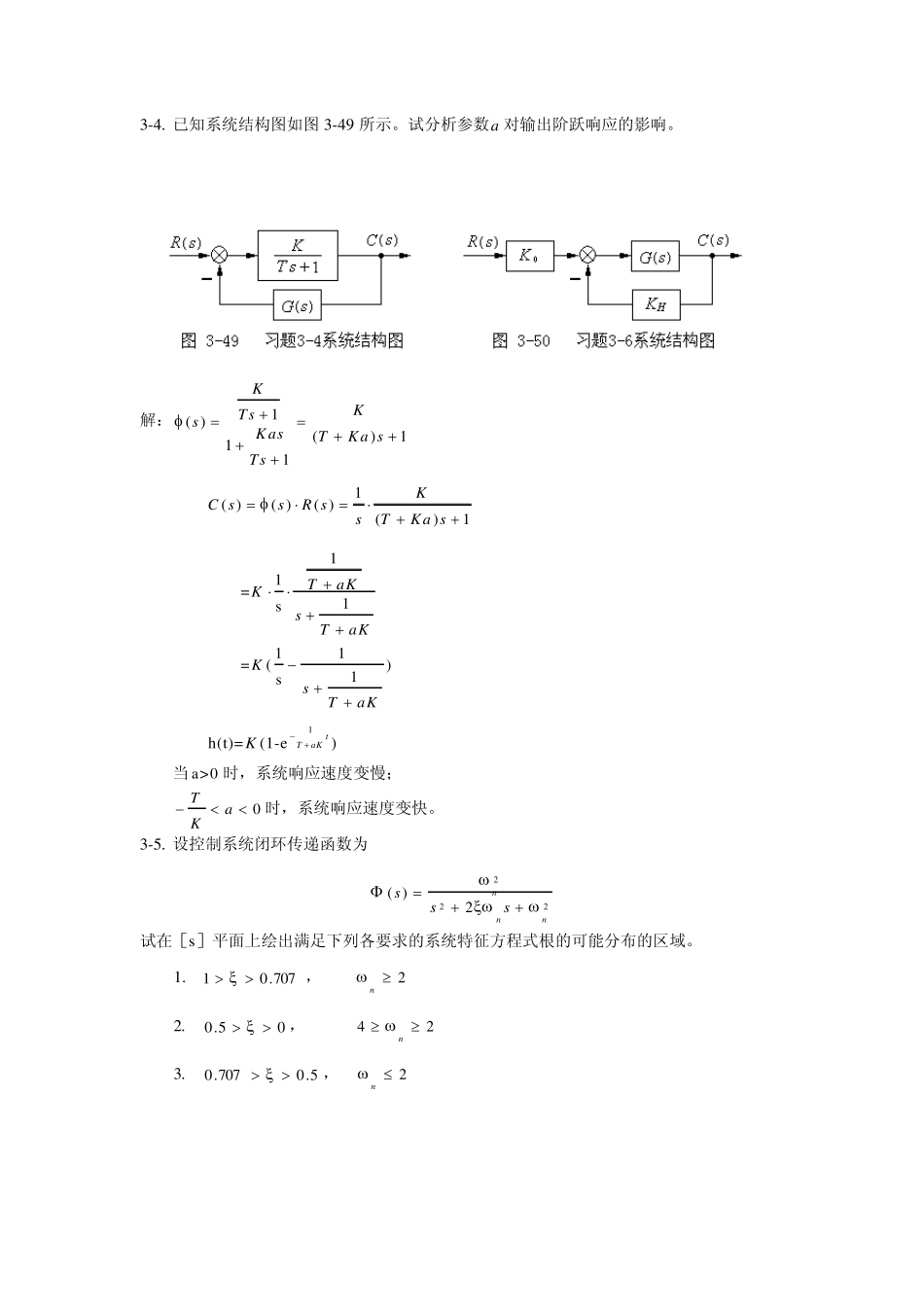
第三章 时域分析法作业与习题解答 3-1. 假设温度计可用11Ts传递函数描述其特性，现在用温度计测量盛在容器内的水温。发现需要 min1时间才能指示出实际水温的98%的数值，试问该温度计指示出实际水温从 10%变化到 90%所需的时间是多少? 解： 41 m i n , = 0 . 2 5TT 1111( )=1-e0.1, =ln 0.9th ttTT 21T22()=0.9=1-e ln 0.1th ttT ， 210.9ln2.20.55 m in0.1rtttTT 3-2. 系统在静止平衡状态下，加入输入信号tttr)(1)(，测得响应为 tettC109.0)9.0()( 试求系统的传递函数。 解：2210.90.910(s+1)( )=10s (s+10)C ssss 22111R (s)=ssss ( )10( )( )10C ssR ss 3-3. 某惯性环节在单位阶跃作用下各时刻的输出值如下表所示。试求环节的传递函数。 t 0 1 2 3 4 5 6 7  h ( t) 0 1.61 2.97 3.72 4.38 4.81 5.10 5.36 6.00 解： 设( )1KsTs 11( )( )( )()1(1)KC ssR sKs TsssT 1( )tTh tKKe ()6hK 1161.61( )661.61, ln0.3126Th teT  6 3.2 ( )3.21Tss 3-4. 已知系统结构图如图3-49 所示。试分析参数a 对输出阶跃响应的影响。 解：1( )()111KKTssKasTKa sTs 1( )( )( )()1KC ssR ssTKa s 11=1sTaKKsTaK 11=()1sKsTaK 1h(t)=(1-e)tTaKK 当 a>0 时，系统响应速度变慢； 0TaK时，系统响应速度变快。 3-5. 设控制系统闭环传递函数为 2222)(nnnsss 试在［s］平面上绘出满足下列各要求的系统特征方程式根的可能分布的区域。 1.707.01 ， 2n 2.05.0 ， 24n 3.5.0707.0 ， 2n 解：① 0.707<<1, 2n ② 0<0.5, 24n ③ 0.50.707, 2n 3-6. 已知某前向通路的传递函数(如图 3-50 所示) 12.010)(ssG 今欲采用负反馈的办法将阶跃响应的调节时间st 减小为原来的1.0倍，并保证总放大系数不变。试选择HK和0K 的值。 解： 00010( )10110( )0.21( )0.21101110HHHHKK G sKKsKG ssKsK 010K101100.2T0.20.10.02110HHKKKK 解得：00.9 =10HKK 题解3-5（1） 题解3-5（2） ...