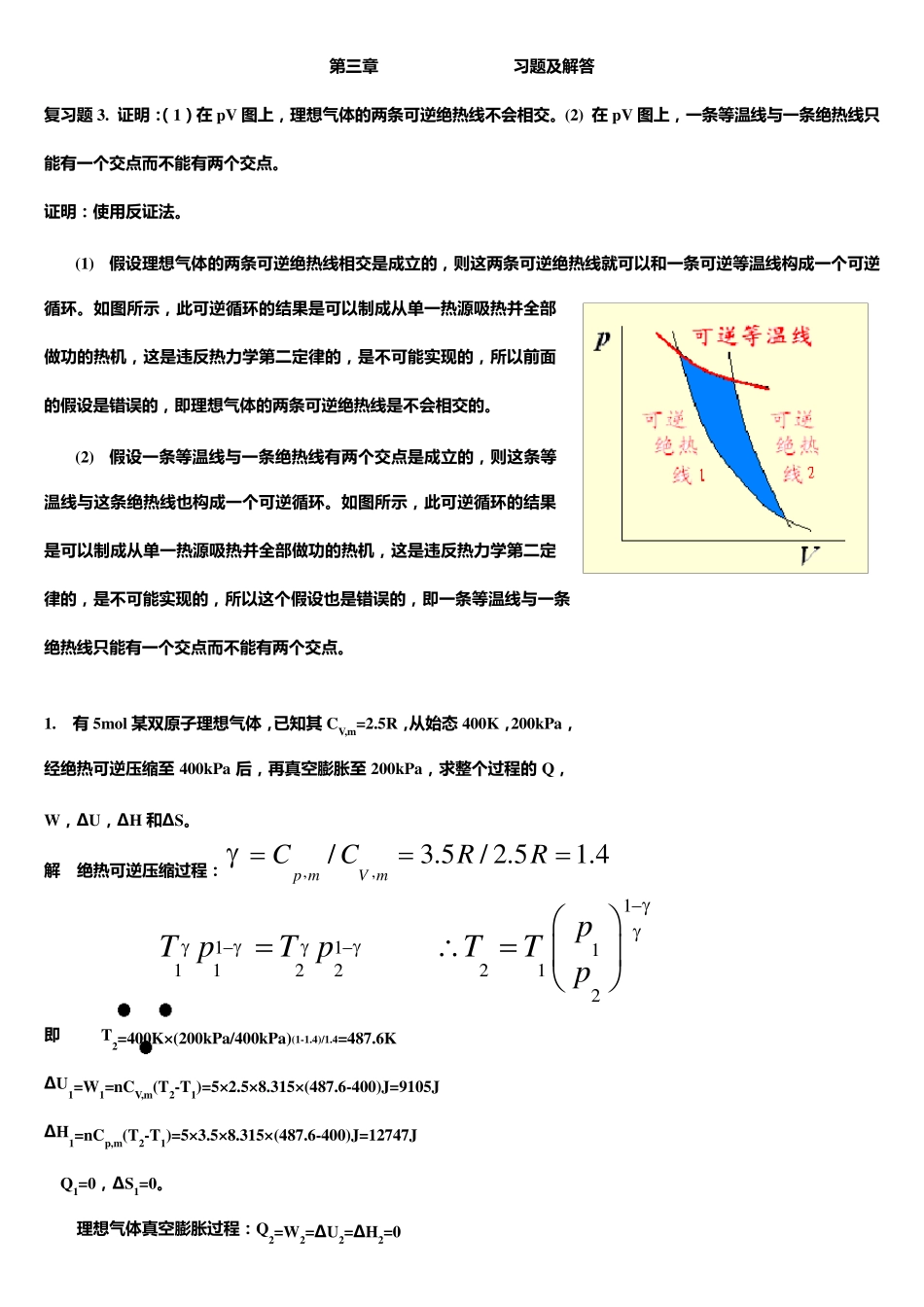
第 三 章 习 题 及 解 答 复 习 题 3. 证 明 :( 1) 在 pV 图 上 , 理 想 气 体 的 两 条 可 逆 绝 热 线 不 会 相 交 。(2) 在 pV 图 上 , 一 条 等 温 线 与 一 条 绝 热 线 只能 有 一 个 交 点 而 不 能 有 两 个 交 点 。 证 明 : 使 用 反 证 法 。 (1) 假 设 理 想 气 体 的 两 条 可 逆 绝 热 线 相 交 是 成 立 的 , 则 这 两 条 可 逆 绝 热 线 就 可 以 和 一 条 可 逆 等 温 线 构 成 一 个 可 逆循 环 。如 图 所 示 , 此 可 逆 循 环 的 结 果 是 可 以 制 成 从 单 一 热 源 吸 热 并 全 部做 功 的 热 机 , 这 是 违 反 热 力 学 第 二 定 律 的 , 是 不 可 能 实 现 的 , 所 以 前 面的 假 设 是 错 误 的 , 即 理 想 气 体 的 两 条 可 逆 绝 热 线 是 不 会 相 交 的 。 (2) 假 设 一 条 等 温 线 与 一 条 绝 热 线 有 两 个 交 点 是 成 立 的 , 则 这 条 等温 线 与 这 条 绝 热 线 也 构 成 一 个 可 逆 循 环 。如 图 所 示 , 此 可 逆 循 环 的 结 果是 可 以 制 成 从 单 一 热 源 吸 热 并 全 部 做 功 的 热 机 , 这 是 违 反 热 力 学 第 二 定律 的 , 是 不 可 能 实 现 的 , 所 以 这 个 假 设 也 是 错 误 的 , 即 一 条 等 温 线 与 一 条绝 热 线 只 能 有 一 个 交 点 而 不 能 有 两 个 交 点 。 1. 有 5mol 某 双 原 子 理 想 气 体 , 已 知 其 CV,m=2.5R, 从 始 态 400K, 200kPa,经 绝 热 可 逆 压 缩 至400kPa 后 , 再 真 空 膨 胀 至 200kPa, 求 整 个 过 程 的Q,W, Δ U, Δ H 和 Δ S。 解 绝 热 可 逆 压 缩 过 程 :,,/3 .5/ 2 .51 .4p mV mCCRR 11111122212pT pT pTTp 即 T2=400K×(200kPa/400kPa)(1-1.4)/1.4=487.6K Δ U1=W1=nCV,m(T2-T1)=5×2.5×8.315×(487.6-400)J=9105J Δ H1=nCp,m(T2-T1)=5×3.5×8.315×(487.6-400)J=12747J Q1=0, Δ S1=0。 理 想 ...