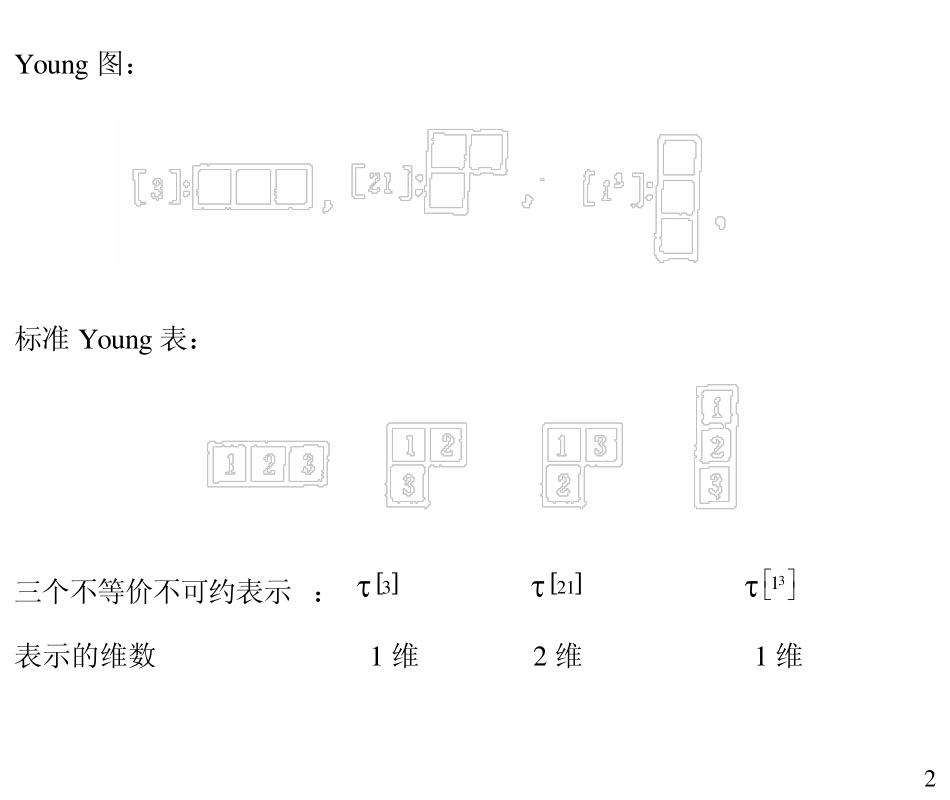
1 §5 Young 图方法应用于寻求置换群的不可约表示 求置换群3S 的所有不等价不可约表示 置换群3S 的群代数 3( )( ){ ( )((12))(12)((13))(13)((23))(23)((123))(123)((132))(132)}st SRt ttCe eϕϕϕϕϕϕϕϕ∈⎧⎫⎪⎪=∈⎨⎬⎪⎪⎩⎭=+++++∑ 正整数3 有三个分拆(三个不等价不可约表示) [ ]3 :3=3 [ ]21 : 3=2+1 31⎡ ⎤⎣ ⎦: 3=1+1+1 2 Young图: 标准 Young表: 三个不等价不可约表示 : [ ]3τ [ ]21τ 31τ ⎡⎤⎣⎦ 表示的维数 1 维 2 维 1 维 3 1.先求[ ]21τ 任取Young图[ ]21 的一个Young表来讨论,我们取Y :于是 {}( ),(13)R Ye= {}( ),(12)C Ye= (13)Pe=+ (12)Qe=− (12)(13)(13)(12)cPQe==−+− (12)(13)(123)e=−+− (12)(13)0 (23)(123)0 (132)e=−++ ⋅−+ ⋅ 3( )t Sc t t∈= ∑ 4 系数如下: t e (12) (13) (23) (123) (132) ( )c t 1 -1 1 0 -1 0 {}( )ssCR cx c xR==∈ ( )C — — 子空间,表示空间。 为求( )C 给出的不可约表示 1) 找出( )C 的一个基向量组 2) 求出3S 的左正则表示的算符对这些基向量的作用 5 注意: 3S 的六个置换给出sR 的自然基,只需在如下形状的向量中找( )C 的基向量 sc ,3sS∈ 即: 3331( )( )()t St St Sscsc t tc t stc s t t−∈∈∈===∑∑∑ 计算当 s 取遍3S 时,诸 sc 的系数1()c s t− 6 例如:求(1 2 )c . 由1(1 2 )(1 2 )− = 331(1 2 )((1 2 ))((1 2 ) )t St Scct tct t−∈∈==∑∑ ((1 2 ))( )(1 2 )((1 3 2 ))(1 3 )((1 2 3 ))(2 3 )((2 3 ))(1 2 3 )((1 3 ))(1 3 2 )cec ecccc=+++++ (1 2 )0 (1 3 )(2 3 )0 (1 2 3 )(1 3 2 )e= − ++ ⋅−+ ⋅+ 其中 ((1 2 ) )ct 中的 (1 2 )t可如下求得 (1 2 )t[](1 2 )(1 2 )(1 3 )(2 3 )(1 2 3 )(1 3 2 )e=+++++ (1 2 )(1 3 2 )(1 2 3 )(2 3 )(1 3 )e=+ ++++ 7 即: (12)(13)0 (2 3 )(123)0 (132)ece=−++ ⋅−+ ⋅ (12)(12)0 (13)(2 3 )0 (123)(132)ce= − ++ ⋅−+ ⋅+ 类似地: (13)(12)(13)0 (2 3 )(123)0 (132)ce=−++ ⋅−+ ⋅ (2 3 )00 (12)(13)(2 3 )(123)(132)ce=⋅ + ⋅−++− (123)00 (12)(13)(2 3 )(123)(132)ce...