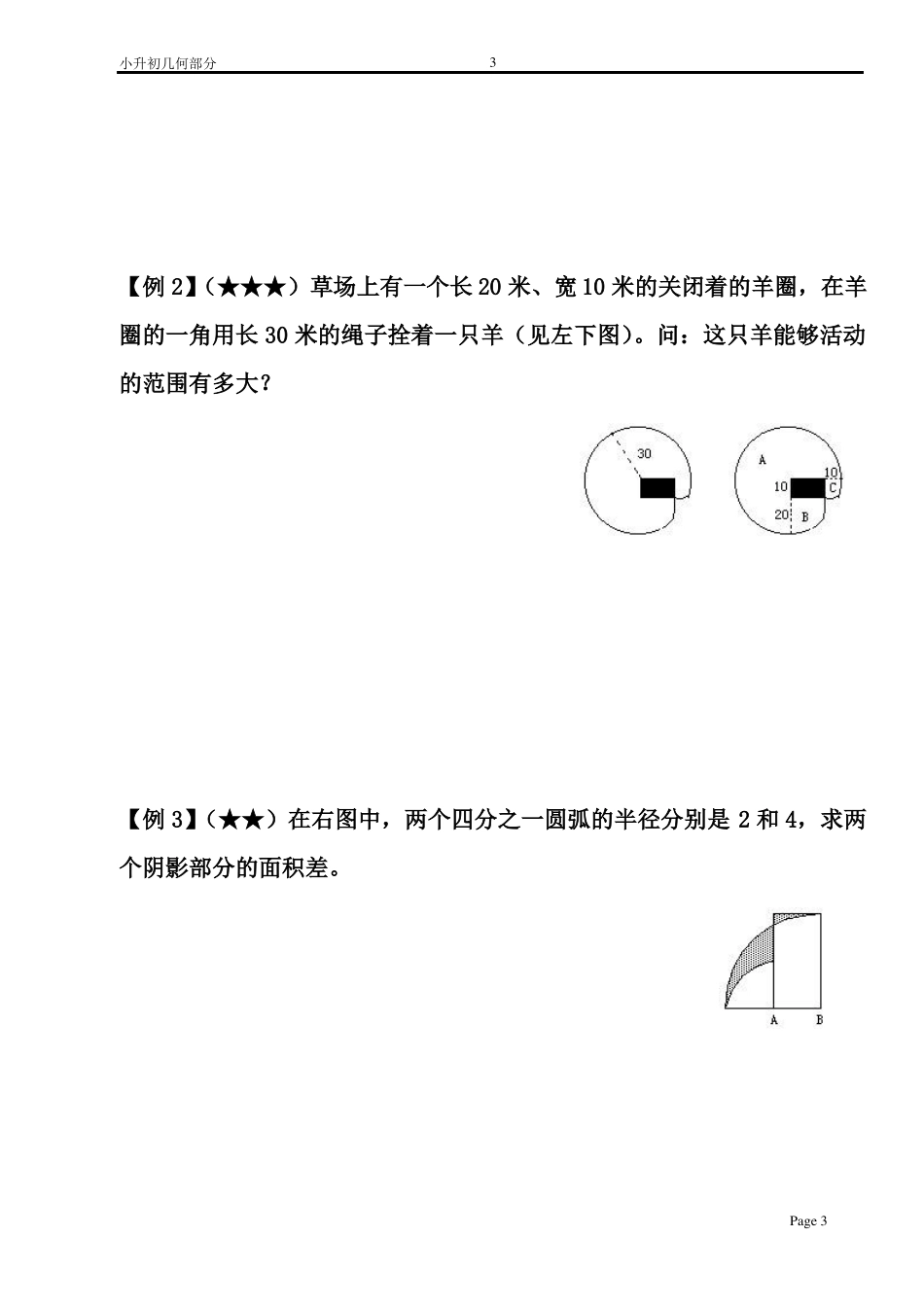
小升初几何部分11 (05 年 101 中学考题)求下图中阴影部分的面积:2 (06 年清华附中考题)从一个长为 8 厘米,宽为 7 厘米,高为 6 厘米的长方体中截下一个最大的正方体,剩下的几何体的表面积是_________平方厘米.3 (06 年三帆中学考试题)有一个棱长为 1 米的立方体,沿长、宽、高分别切二刀、三刀、四刀后,成为 60 个小长方体(见左下图).这 60 个小长方体的表面积总和是______平方米.4(06 年西城八中考题)右上图中每个小圆的半径是 1 厘米,阴影部分的周长是_______厘米.( =3.14)Page 1小升初几何部分25(05 年首师附中考题)一千个体积为 1立方厘米的小正方体合在一起成为一个边长为 10厘米的大正方体,大正方体表面涂油漆后再分开为原来的小正方体,这些小正方体至少有一面被油漆涂过的数目是多少个?第二讲小升初专项训练几何篇(二】1与圆和扇形有关的题型【例 1】(★★)如下图,等腰直角三角形 ABC 的腰为 10厘米;以 A 为圆心,EF 为圆弧,组成扇形 AEF;阴影部分甲与乙的面积相等。求扇形所在的圆面积。Page 2小升初几何部分3【例 2】(★★★)草场上有一个长 20 米、宽 10 米的关闭着的羊圈,在羊圈的一角用长 30 米的绳子拴着一只羊(见左下图)。问:这只羊能够活动的范围有多大?【例 3】(★★)在右图中,两个四分之一圆弧的半径分别是 2 和 4,求两个阴影部分的面积差。Page 3小升初几何部分4【例 4】(★★★)如图,ABCD 是正方形,且 FA=AD=DE=1,求阴影部分的面积。(取π=3)【例 5】(★★★)如下图,AB 与 CD 是两条垂直的直径,圆 O 的半径为15 厘米,Page 4小升初几何部分5求不规则立体图形的表面积与体积【例 6】(★★)用棱长是 1 厘米的正方块拼成如下图所示的立体图形,问该图形的表面积是多少平方厘米?【例 7】(★★★)在边长为 4 厘米的正方体木块的每个面中心打一个边与正方体的边平行的洞.洞口是边长为 1 厘米的正方形,洞深 1 厘米(如下图).求挖洞后木块的表面积和体积.【例 8】(★★★)如图是一个边长为 2 厘米的正方体。在正方体的上面的正中向下挖一个边长为 1 厘米的正方体小洞;接着在小洞的底面正中再向下挖一个边长为 1/2 厘米的小洞;第三个小洞的挖法与前两个相同,边长为 1/4 厘米。那么最后得到的立体图形的表面积是多少平方厘米?Page 5小升初几何部分63水位问题【例 9】(★★)一个酒...