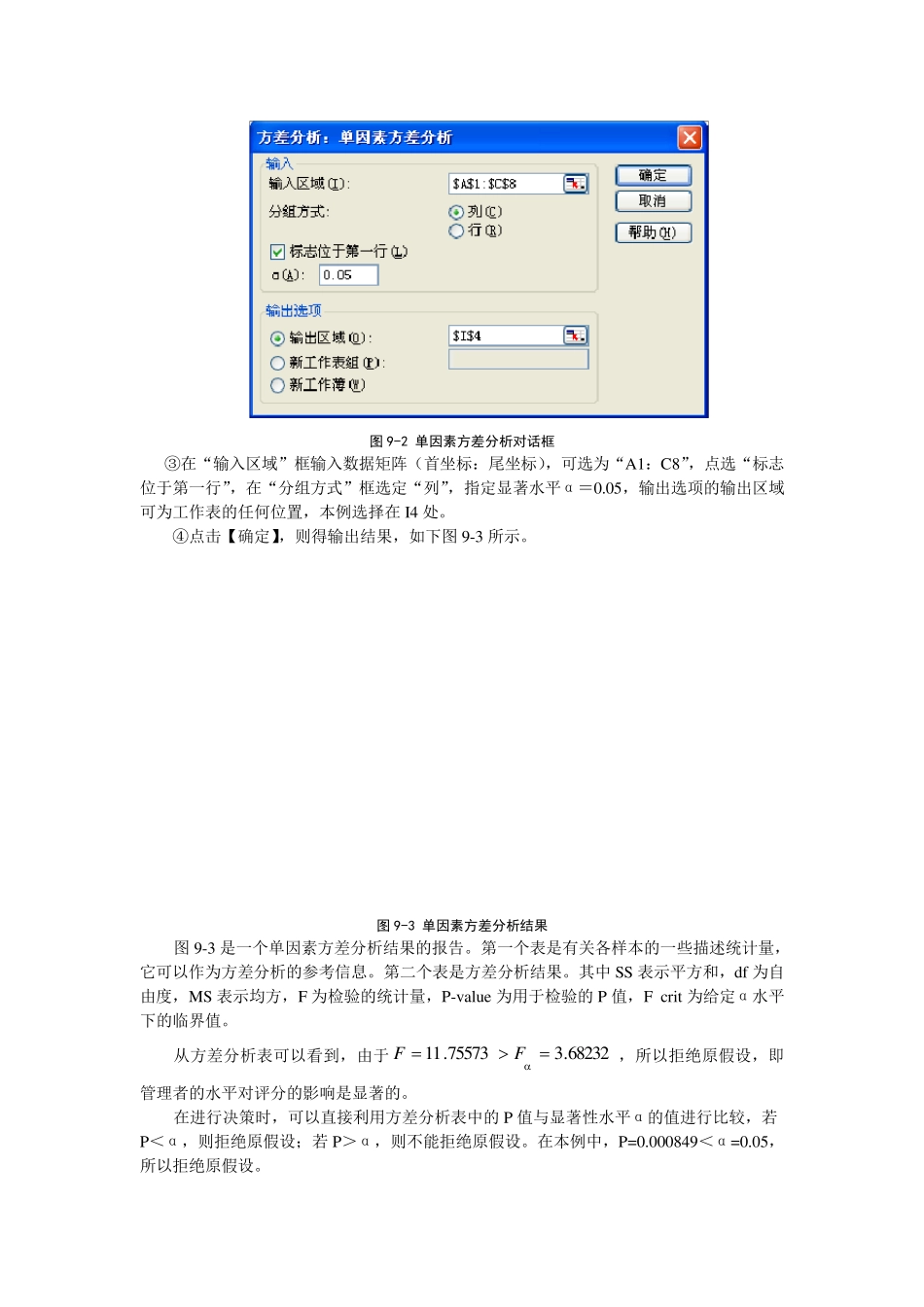
方差分析 1、单因素方差分析 例1:一家管理咨询公司为不同的客户进行人力资源管理讲座。每次讲座的内容基本上是一样的,但讲座的听课者有时是高级管理者,有时是中级管理者,有时是低级管理者。该咨询公司认为,不同层次的管理者对讲座的满意度是不同的。听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1 所示(评分标准从1~10,10 代表非常满意)。 表 9-1 管理者的评分 高级管理者 中级管理者 低级管理者 7 8 5 7 9 6 8 8 5 7 10 7 9 9 4 10 8 8 取显著性水平α=0.05,检验管理者的水平不同是否会导致评分的显著性差异? 首先提出假设 H0:管理者的水平对评分没有显著影响。 操作步骤: ①输入数据,如图 9-1 所示: ②在菜单中,选取【工具】→【数据分析】,选定【方差分析:单因素方差分析】,点击【确定】,显示【单因素方差分析】对话框,如图 9-2。 图 9-1 管理者的评分数据 图9-2 单因素方差分析对话框 ③在“输入区域”框输入数据矩阵(首坐标:尾坐标),可选为“A1:C8”,点选“标志位于第一行”,在“分组方式”框选定“列”,指定显著水平α=0.05,输出选项的输出区域可为工作表的任何位置,本例选择在I4 处。 ④点击【确定】,则得输出结果,如下图 9-3 所示。 图9-3 单因素方差分析结果 图 9-3 是一个单因素方差分析结果的报告。第一个表是有关各样本的一些描述统计量,它可以作为方差分析的参考信息。第二个表是方差分析结果。其中 SS 表示平方和,df 为自由度,MS 表示均方,F 为检验的统计量,P-v alu e 为用于检验的 P 值,F crit 为给定α水平下的临界值。 从方差分析表可以看到,由于68232.375573.11FF,所以拒绝原假设,即管理者的水平对评分的影响是显著的。 在进行决策时,可以直接利用方差分析表中的 P 值与显著性水平α的值进行比较,若 P<α,则拒绝原假设;若 P>α,则不能拒绝原假设。在本例中,P=0.000849<α=0.05,所以拒绝原假设。 2、双因素无重复试验的方差分析 例2:有4 个品牌的洗衣机在5 个地区销售,为分析洗衣机的品牌和销售地区对销售量的影响,对每个品牌在各地区的销售量取得以下数据(单位:台)。试分析品牌和销售地区对洗衣机的销售量是否有显著影响?(α=0.05) 首先对行因素和列因素分别提出假设: H01:品牌因素对洗衣机销售量没有显著影响 H02:地区因素对洗衣机销售量没有显著影响 地...