异面直线成角求法

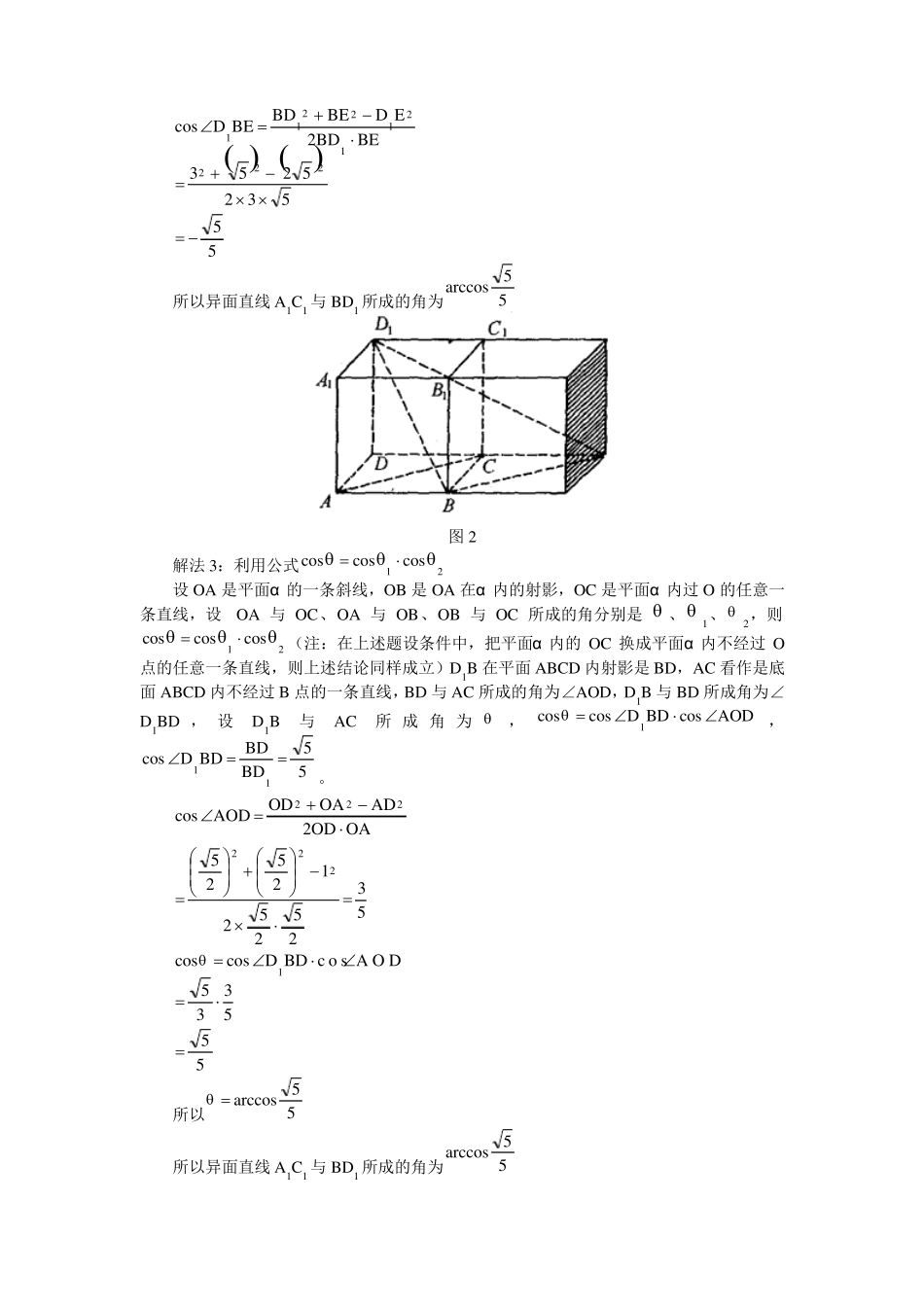
求异面直线所成的角求异面直线所成的角，一般有两种方法，一种是几何法，这是高二数学人教版（A）版本倡导的传统的方法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求。还有一种方法是向量法，即建立空间直角坐标系，利用向量的代数法和几何法求解，这是高二数学人教版（B）倡导的方法，下面举例说明两种方法的应用。例：长方体 ABCD－A1B1C1D1 中，AB=AA1=2cm，AD=1cm，求异面直线 A1C1 与 BD1 所成的角。解法 1：平移法设 A1C1 与 B1D1 交于 O，取B1B 中点 E，连接OE，因为OE//D1B，所以∠C1OE 或其补角就是异面直线 A1C1 与 BD1 所成的角△C1OE 中15A1C1 22113OE BD1 22  22 1 222OC1 222C E B C B E 1 1 211112OC1  OE 2  C1E 2所以cosC1OE 2OC1  OE225 3  2    2 532225 52 225所以C1OE  a r c c o s5所以异面直线A1C1与BD1所成的角为arccos55图 1解法 2：补形法在长方体 ABCD—A1B1C1D1 的面 BC1上补上一个同样大小的长方体，将 AC 平移到 BE，则∠D1BE 或其补角就是异面直线 A1C1 与 BD1 所成的角，在△BD1E 中，BD1=3，BE 5 ，D1E 42  22  2 5BD1  BE 2  D1E 2cosD1BE 2BD1  BE 32 552 5 2 5222 35 所以异面直线 A1C1 与 BD1 所成的角为arccos55图 2解法 3：利用公式cos  cos1  cos2设 OA 是平面α 的一条斜线，OB 是 OA 在α 内的射影，OC 是平面α 内过 O 的任意一条直线，设OA 与 OC、OA 与 OB、OB 与 OC 所成的角分别是  、1、2，则cos  cos1  cos2 （注：在上述题设条件中，把平面α 内的 OC 换成平面α 内不经过 O点的任意一条直线，则上述结论同样成立）D1B 在平面 ABCD 内射影是 BD，AC 看作是底面 ABCD 内不经过 B 点的一条直线，BD 与 AC 所成的角为∠AOD，D1B 与 BD 所成角为∠D1BD ， 设D1B与AC所 成 角 为 ， cos  cos D1BD  cos AOD，cos D1BD  BD5BD15 。OD2  OA 2  AD2cosAOD 2OD  OA5   5  12 2  2 3 55...