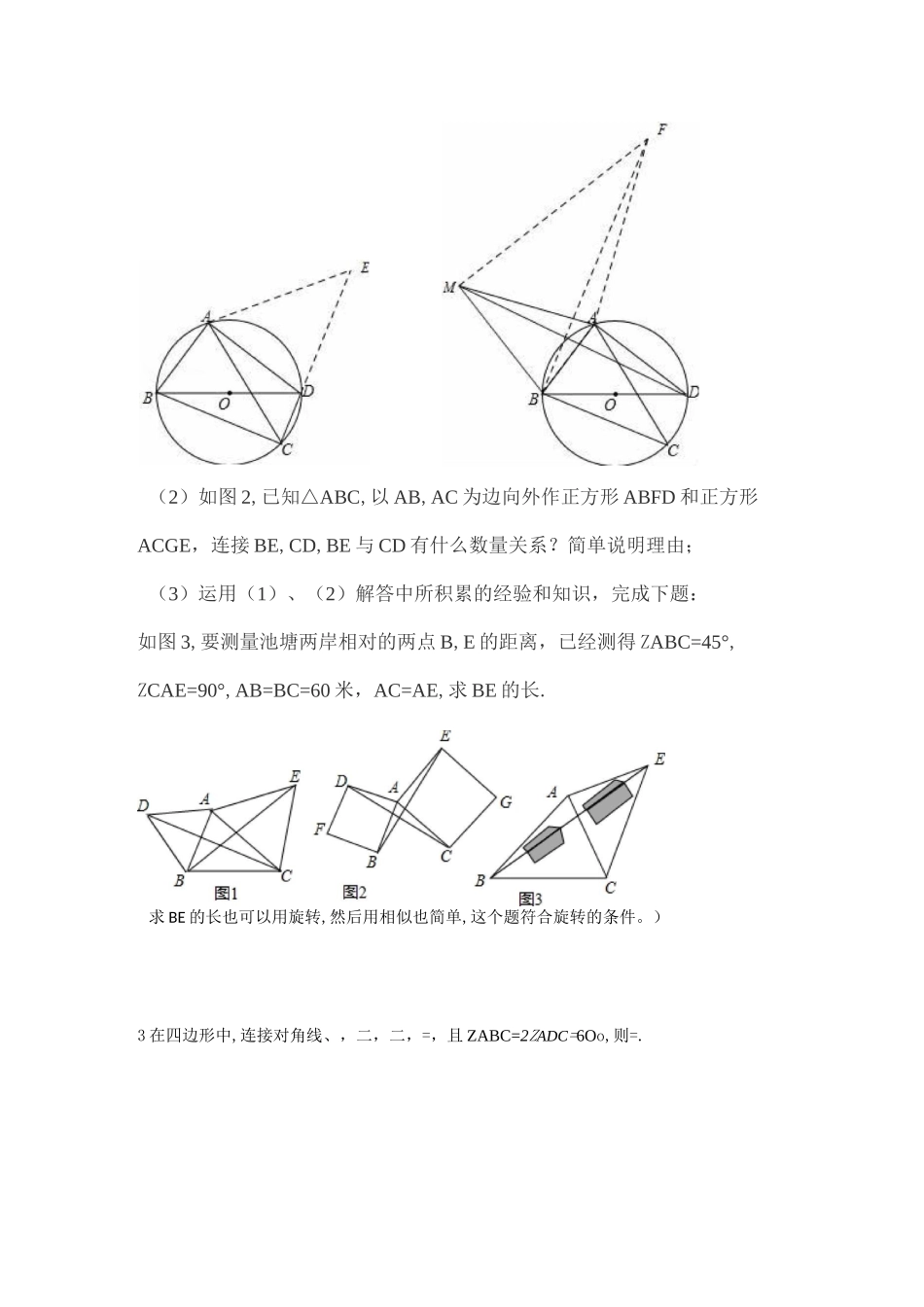
1.如图,点 C 为 ABD 的外接圆上的一动点(点 C 不在 AE 匚上,且不与点 B,D 重合),ZACB=ZABD=45°(1) 求证:BD 是该外接圆的直径;(2) 连结 CD,求证:月 AC=BC+CD;(3) 若厶 ABC 关于直线 AB 的对称图形为△ABM,连接 DM,试探究 DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.【分析】(1)要证明 BD 是该外接圆的直径,只需要证明 ZBAD 是直角即可,又因为ZABD=45°,所以需要证明 ZADB=45°;(2)在 CD 延长线上截取 DE=BC,连接 EA,只需要证明△EAF 是等腰直角三角形即可得出结论;(3)过点 M 作 MF 丄 MB 于点 M,过点 A 作 AF 丄 MA 于点 A,MF 与 AF 交于点 F,证明△AMF是等腰三角形后,可得出 AM=AF,MF=;2AM,然后再证明△ABF^^ADM 可得出 BF=DM,最后根据勾股定理即可得出 DM2,AM2,BM2三者之间的数量关系.2.(1)如图 1,已知△ABC,以 AB,AC 为边向△ABC 外做等边厶 ABD 和等边△ACE,连接BE,CD,求证:BE 二CD;(2)如图 2,已知△ABC,以 AB,AC 为边向外作正方形 ABFD 和正方形ACGE,连接 BE,CD,BE 与 CD 有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图 3,要测量池塘两岸相对的两点 B,E 的距离,已经测得 ZABC=45°,ZCAE=90°,AB=BC=60 米,AC=AE,求 BE 的长.求 BE 的长也可以用旋转,然后用相似也简单,这个题符合旋转的条件。)3 在四边形中,连接对角线、,二,二,=,且 ZABC=2ZADC=6Oo,则=.在四边形中,、是对角线,△是等边三角形,Z=30°,=3,则的长为()5 已知:在厶中,Z=60°.(1) 如图 1,若=,点在厶内,且 Z=150°,=,二,把厶绕着点顺时针旋转,使点旋转到点处,得到△,连接① 依题意补全图 1;② 直接写出的长;(2) 如图 2,若=,点在△外',且=,=5,=,求 Z 的度数;()如图,若=2,点在厶内,且=<3,=5,Z=120°,请直接写出的长.7.(2017・绥化)在平面直角坐标系中,直线-1 交轴于点,交轴于点,抛物线-122经过点,与直线-交于点(,-2).(1)求抛物线的解析式;(2)如图,横坐标为的点在直线上方的抛物线上,过点作 II轴交直线于点,以为直径的圆交直线于另一点,当点在轴上时,求△的周长.()将公绕坐标平面内的某一点按顺时针方向旋转 90°,得到△111,点,,的对应点分别是点 1,1,],若△]]]的两个顶点恰好落在抛物线上,请直接写出点/勺坐标.8 探究发现:下面是一道例题及其...