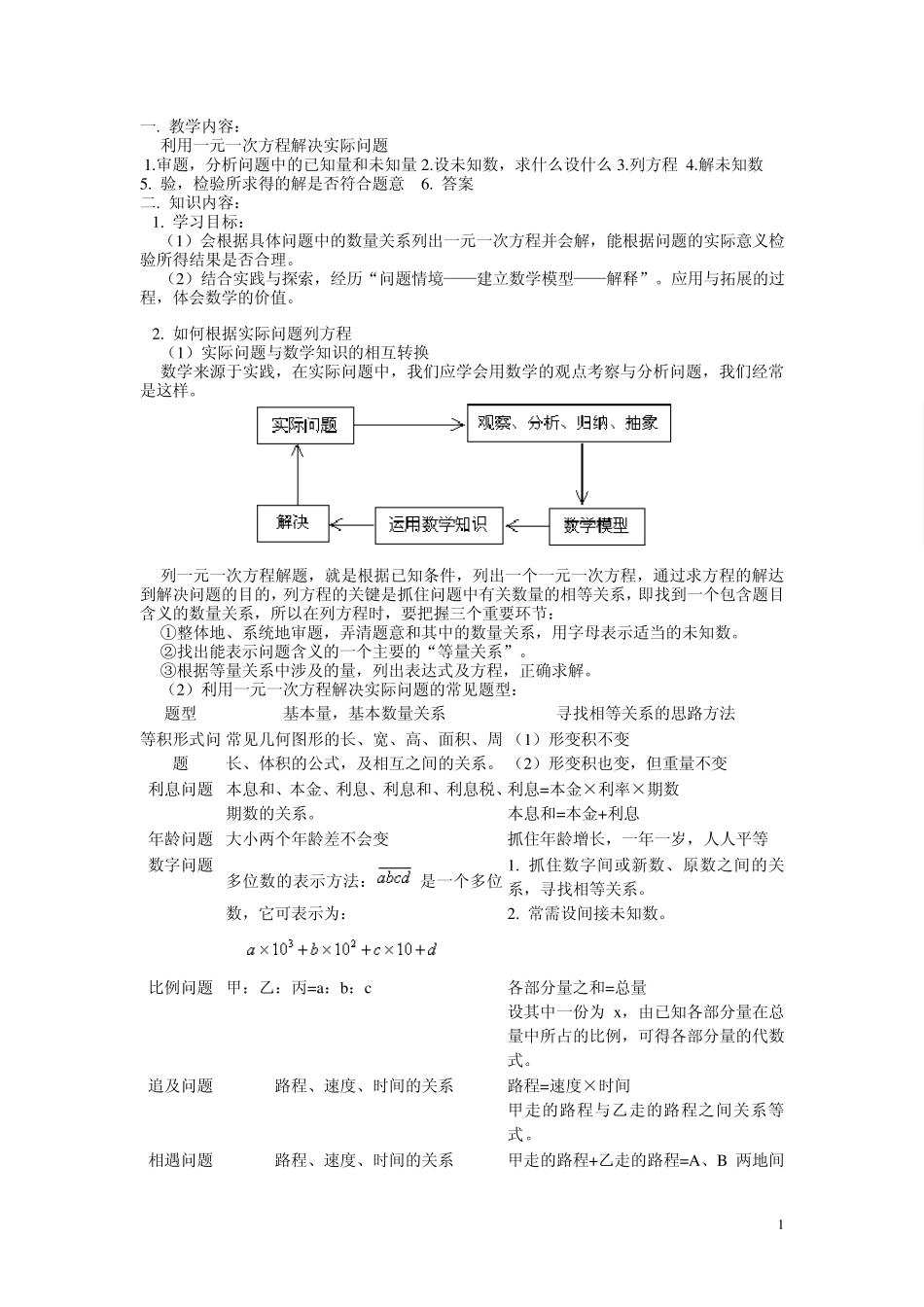
1 一. 教学内容: 利用一元一次方程解决实际问题 1.审题,分析问题中的已知量和未知量 2.设未知数,求什么设什么 3.列方程 4.解未知数 5. 验,检验所求得的解是否符合题意 6. 答案 二. 知识内容: 1. 学习目标: (1)会根据具体问题中的数量关系列出一元一次方程并会解,能根据问题的实际意义检验所得结果是否合理。 (2)结合实践与探索,经历“问题情境——建立数学模型——解释”。应用与拓展的过程,体会数学的价值。 2. 如何根据实际问题列方程 (1)实际问题与数学知识的相互转换 数学来源于实践,在实际问题中,我们应学会用数学的观点考察与分析问题,我们经常是这样。 列一元一次方程解题,就是根据已知条件,列出一个一元一次方程,通过求方程的解达到解决问题的目的,列方程的关键是抓住问题中有关数量的相等关系,即找到一个包含题目含义的数量关系,所以在列方程时,要把握三个重要环节: ①整体地、系统地审题,弄清题意和其中的数量关系,用字母表示适当的未知数。 ②找出能表示问题含义的一个主要的“等量关系”。 ③根据等量关系中涉及的量,列出表达式及方程,正确求解。 (2)利用一元一次方程解决实际问题的常见题型: 题型 基本量,基本数量关系 寻找相等关系的思路方法 等积形式问题 常见几何图形的长、宽、高、面积、周长、体积的公式,及相互之间的关系。 (1)形变积不变 (2)形变积也变,但重量不变 利息问题 本息和、本金、利息、利息和、利息税、期数的关系。 利息=本金×利率×期数 本息和=本金+利息 年龄问题 大小两个年龄差不会变 抓住年龄增长,一年一岁,人人平等 数字问题 多位数的表示方法:是一个多位数,它可表示为: 1. 抓住数字间或新数、原数之间的关系,寻找相等关系。 2. 常需设间接未知数。 比例问题 甲:乙:丙=a:b:c 各部分量之和=总量 设其中一份为 x,由已知各部分量在总量中所占的比例,可得各部分量的代数式。 追及问题 路程、速度、时间的关系 路程=速度×时间 甲走的路程与乙走的路程之间关系等式。 相遇问题 路程、速度、时间的关系 甲走的路程+乙走的路程=A、B 两地间 2 的路程 航行问题 顺水速度、静水速度、水流速度、时间、路程、速度之间的关系。 两地间距离不变 顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度 (3)设未知数的方法: 根据具体问题作具体分析,设未知数通常有两种方法: ①直接设...