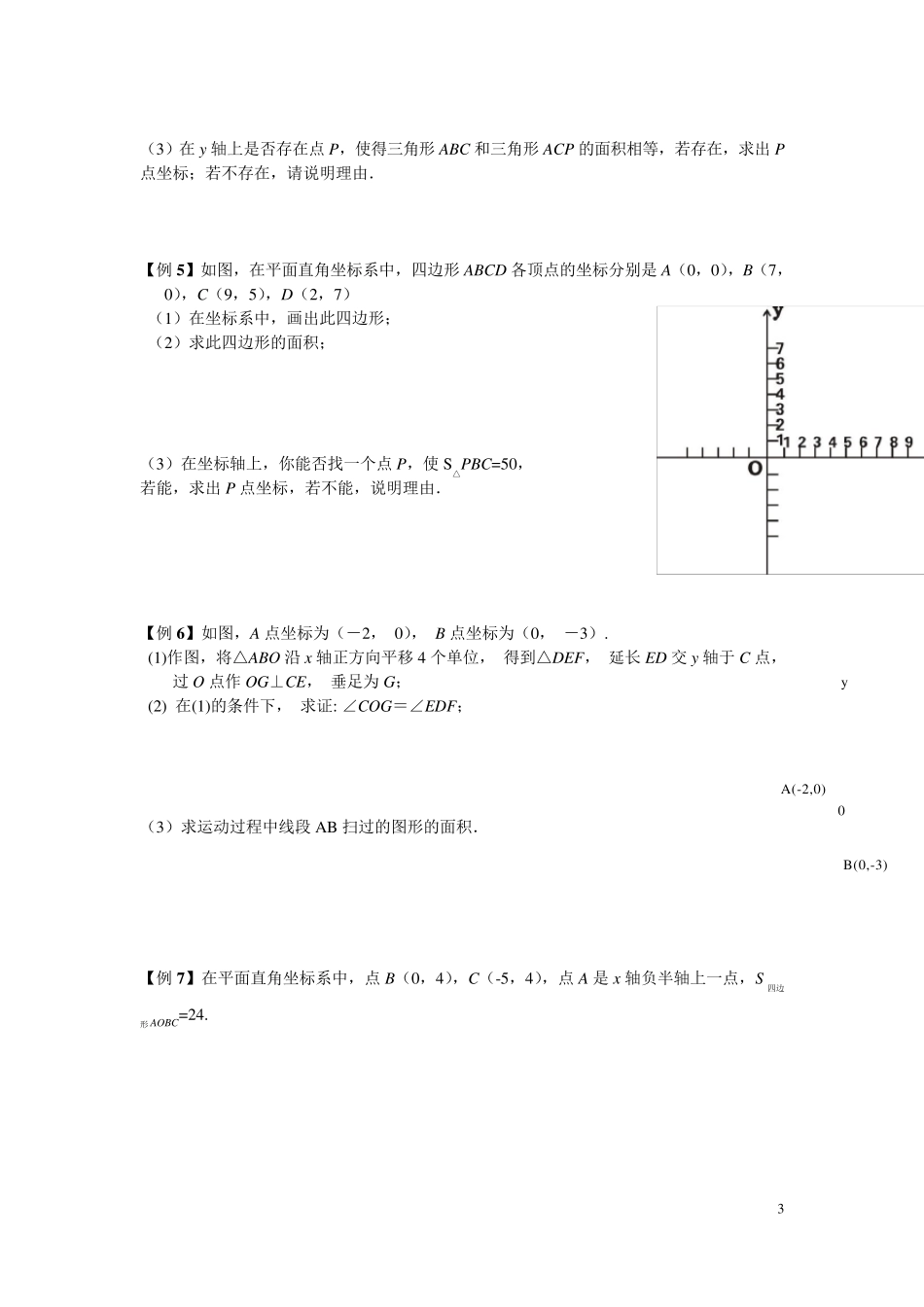
1 培优训练三:平面直角坐标系(压轴题) 一、坐标与面积: 【例1】如图,在平面直角坐标中,A(0,1),B(2,0),C(2,1.5). (1)求△ABC 的面积; (2)如果在第二象限内有一点 P(a,0.5),试用 a 的式子表示四边形 ABOP 的面积; (3)在(2)的条件下,是否存在这样的点 P,使四边形 ABOP 的面积与△ABC 的面积相等?若存在,求出点 P 的坐标,若不存在,请说明理由. yxPOCBA 【例2】在平面直角坐标系中,已知 A(-3,0),B(-2,-2),将线段 AB 平移至线段 CD. 图1yxDOCBA图2yxDOCBA图3yxOBA图4yxOBA (1)如图1,直接写出图中相等的线段,平行的线段; (2)如图2,若线段 AB 移动到 CD,C、D 两点恰好都在坐标轴上,求C、D 的坐标; (3)若点 C 在y 轴的正半轴上,点 D 在第一象限内,且 S△ACD=5,求C、D 的坐标; (4)在y 轴上是否存在一点 P,使线段 AB 平移至线段 PQ 时,由 A、B、P、Q 构成的四边形是平行四边形面积为 10,若存在,求出 P、Q 的坐标,若不存在,说明理由; 2 【例3】如图,△ABC 的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0). (1)求△ABC 的面积; (2)若把△ABC 向下平移2 个单位长度,再向右平移3 个单位长度,得到△A B C ,请你在图中画出△A B C ; (3)若点A、C 的位置不变,当点P 在y 轴上什么位置时,使2ACPABCSS; (4)若点B、C 的位置不变,当点Q 在x 轴上什么位置时,使2BCQABCSS. 【例4 】如图1 ,在平面直角坐标系中,A(a,0 ),C(b,2 ),且满足 2(2 )20ab,过C 作CB⊥x 轴于B. (1 )求三角形ABC 的面积; (2 )若过B 作BD∥AC 交y 轴于D,且AE,DE 分别平分∠CAB,∠ODB,如图2 ,求∠AED的度数; 3 (3)在y 轴上是否存在点P,使得三角形ABC 和三角形ACP 的面积相等,若存在,求出P点坐标;若不存在,请说明理由. 【例5】如图,在平面直角坐标系中,四边形ABCD 各顶点的坐标分别是A(0,0),B(7,0),C(9,5),D(2,7) (1)在坐标系中,画出此四边形; (2)求此四边形的面积; (3)在坐标轴上,你能否找一个点P,使S△PBC=50, 若能,求出P 点坐标,若不能,说明理由. 【例6】如图,A 点坐标为(-2, 0), B 点坐标为(0, -3). (1)作图,将△ABO 沿x 轴正方向平移4 个单位, 得到△DEF,...