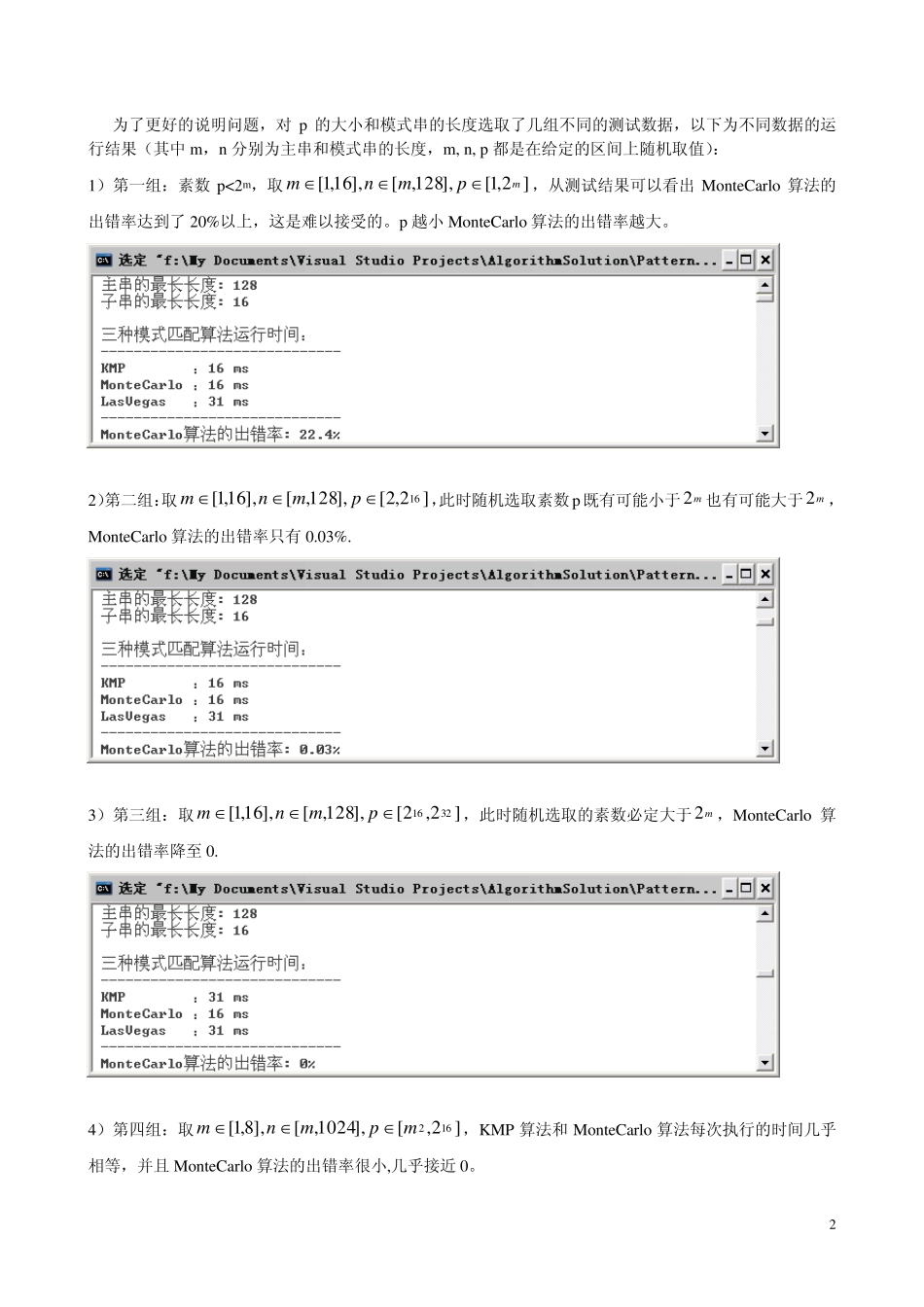
1 三种模式匹配算法 作业要求:分别用KMP、MonteCarlo、LasVegs算法编制三个程序,随机生成不小于 5000对长度不等的 01串(三个程序使用相同的串),然后统计算法的执行时间和 MonteCarlo算法的出错比率,并根据运行结果对三种算法进行深入的比较。 1、 算法思路 KMP 算法的主要特点是指向主串的指针不需要回溯,只向右移动,即模式串在与主串失配时,并不回溯主串的指针与模式串重新匹配,而是根据已经得到的匹配信息将模式串尽可能远的向右滑动一段。滑动距离的大小取决于模式串的失效函数next, next[k](0<=k<=m-1)的值表示当模式串在下标为k 的字符处与主串失配时应该向右移动到下标为next[k]的字符处再与主串重新匹配。算法首先要求模式串的失效函数next,然后再根据next 的值进行模式匹配,在最坏情况下的时间复杂度为O(m*n),m 为模式串的长度,n 为主串的长度,当如果模式串中有较多相同的字符时,时间复杂度一般可达到O(m+n)。 MonteCarlo 随机算法主要是通过比较模式串和主串中与模式串等长的串的“指纹”来匹配的,若两者指纹相等,则可以认为在概率意义下两者是相等的,算法中要求用到一个随机产生的素数作模运算,该素数的选取直接影响了算法的准确率,算法的时间复杂度为O(m+n)。但有一定的出错率,即选取主串中比较串的指纹与模式串相等时但比较串与模式串并不相等,理论上这种情况出现的概率为1/n,只与主串的长度有关,与模式串的长度无关,但实际上只要选取素数合适出错率比1/n 要小的多。 LasVegas 算法是对 MonteCarlo 算法的改进,当模式串的指纹与主串中的比较串相等时,此时并不直接返回匹配的位置,而是判断两个字符串是否真的相等,相等则返回,否则继续匹配。所以,该算法总能得到正确的位置,但算法的执行时间稍微比MonteCarlo 算法要长一点(判断字符串是否相等的耗费),时间复杂度的期望值不超过O(m+n)。 要完成上述三个模式匹配算法的比较,需要一个 0/1 串的随机发生器和一个素数发生器。程序中头文件”randstr.h”包含的RandomString 类是用来产生 MAXSIZE 对的主串和模式串的,0/1 串的长度和内容都是随机的,为了便于比较,规定主串的长度一定大于模式串的长度。”random.h”包含的Random 类封装了产生随机数的函数。素数发生器首先产生 MAXSIZE 个随机数保存在prime 数组中,供随机算法使用。本程序中随机生成了 10000 对 0/1 串作为测试数据,即MAXSIZE=10000。...