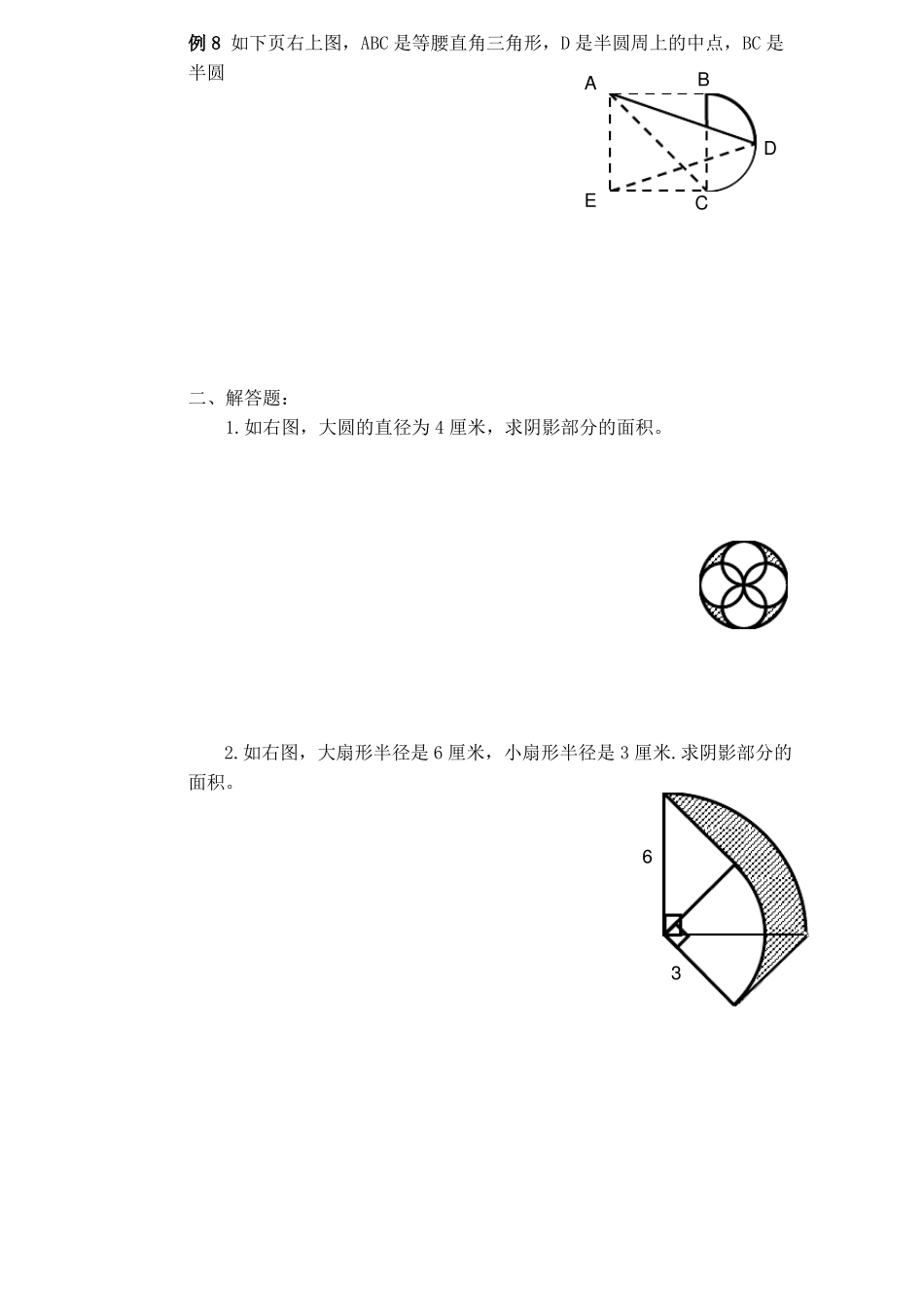
圆和扇形的面积计算三姓名不规则图形的另外一种情况,就是由圆、扇形、弓形与三角形、正方形、长方形等规则图形组合而成的,这是一类更为复杂的不规则图形,为了计算它的面积,常常要变动图形的位置或对图形进行适当的分割、拼补、旋转等手段使之转化为规则图形的和、差关系,同时还常要和“容斥原理”(即:集合 A 与集合 B 之间有:SA∪B=SA+Sb-SA∩B)合并使用才能解决。例 1 如右图,在一个正方形内,以正方形的三条边为直径向内作三个半圆.求阴影部分的面积。解法 1:把上图靠下边的半圆换成(面积与它相等)右边的半圆,得到右图.这时,右图中阴影部分与不含阴影部分的大小形状完全一样,因此它们的面积相等.所以上图中阴影部分的面积等于正方形面积的一半。解法 2:将上半个“弧边三角形”从中间切开,分别补贴在下半圆的上侧边上,如右图所示.阴影部分的面积是正方形面积的一半。解法 3:将下面的半圆从中间切开,分别贴补在上面弧边三角形的两侧,如右图所示.阴影部分的面积是正方形的一半.例 2 如右图,正方形 ABCD 的边长为 4 厘米,分别以 B、D 为圆心以 4 厘米为半径在正方形内画圆,求阴影部分面积。A D例 3 如右图,矩形 ABCD 中,AB=6 厘米,BC=4 厘米,扇形 ABE 半径 AE=6 厘米,扇形 CBF 的半 CB=4 厘米,求阴影部分的面积。ADEF例 4 如右图,直角三角形 ABC 中,AB 是圆的直径,且 AB=20 厘米,如果阴影(Ⅰ)的面积比阴影(Ⅱ)的面积大 7 平方厘米,求 BC 长。例 5 如右图,两个正方形边长分别是 10 厘米和 6 厘米,求阴影部分的面积。例 6 如右图,将直径 AB 为 3 的半圆绕 A 逆时针旋转 60°,此时 AB 到达 AC的位置,求阴影部分的面积(取π=3).例 7 如右图,ABCD 是正方形,且 FA=AD=DE=1,求阴影部分的面积.BFADECE例 8 如下页右上图,ABC 是等腰直角三角形,D 是半圆周上的中点,BC 是半圆二、解答题:ABDEC1.如右图,大圆的直径为 4 厘米,求阴影部分的面积。2.如右图,大扇形半径是 6 厘米,小扇形半径是 3 厘米.求阴影部分的面积。633.如左图,三个同心圆的半径分别是 2、6、10,求 B 中阴影部分占大圆面积的百分之几?4.如右图,正方形 ABCD 边长为 1 厘米,依次以 A、B、C、D 为圆心,以 AD、BE、CF、DG 为半径画出扇形,求阴影部分的面积.FADF5.如下图(a),求阴影部分的面积。OMNWA7.如下图(a),△ABC 是...