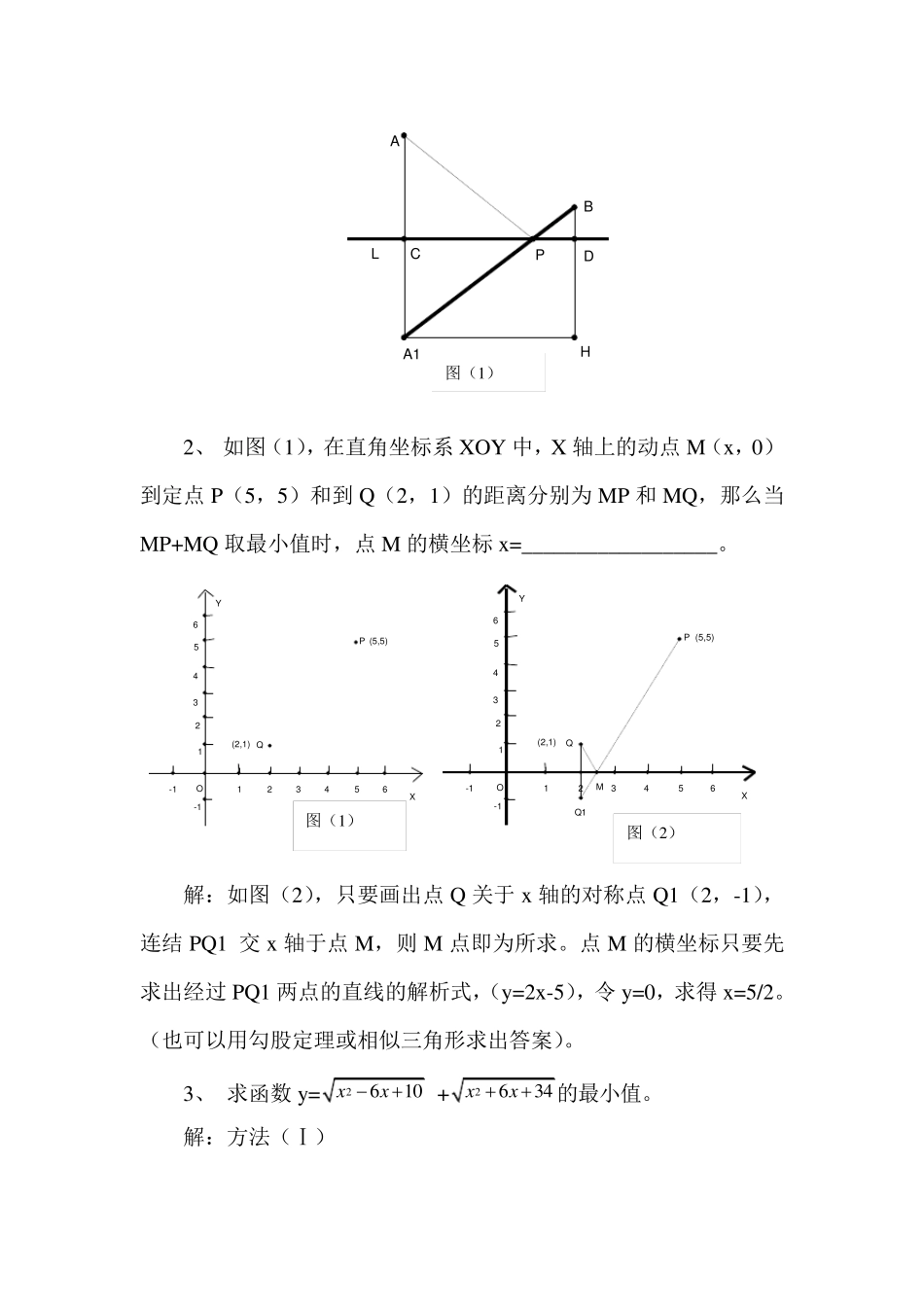
两线段和最小 求线段和的最小值问题,在初中数学中经常会遇到,利用轴对称知识可以比较简单的解决。我们先通过一个非常典型的例题来推导一个性质: 一、性质推导 例题:如图所示,在河岸 L 的一侧有两个村庄 A、B,现要在河岸 L 上修建一个供水站,问供水站应建在什么地方,才能到A,B 两村庄的距离之和最短? 首先,我们来推导一个轴对称的性质,如图,作 B 点关于 L 的对称点 B1, 在直线L 上任意定一点 M,连接 B B1,BM,B1M,根据轴对称知识,我们可以求证 BM=B1M, 所以,我们可以得出这样的性质:成轴对称的两个对应点到对称轴上任意一点的距离相等。 在该例题中,利用这一性质,我们可得出:点 B 到河岸 L 上任意点 M 的距离等于对称B1 到点 M 的距离。 要使 AM+ B1M 最小,必须使 A、M、B1 三点共线, 也就是说,必须使点 M,与 A B1 连线和L 的交点 N重合, 所以,河岸上的N点为到A、B 的距离之和最小的点。 证明:M 为L 上的任意点 因为BM=B1M 所以,BM+AM=B1M+AM,而B1M+AM 大于B1A, 所以,结论成立 二、应用 1 :在图(1)中,若 A 到直线 L 的距离 AC 是 3 千米,B 到直线 L 的距离 BD 是 1 千米,并且 CD 的距离 4 千米,在直线 L 上找一点P,使 PA+PB 的值最小。求这个最小值。 解:作出 A1B(作法如上图) 过 A1 点画直线 L 的平行线与 BD 的延长线交于H, 在 Rt△A1BH 中,A1H=4 千米,BH=4 千米, 用勾股定理求得 A1B 的长度为4 2 千米, 即 PA+PB 的最小值为4 2 千米。 LNOB1BAM 2、 如图(1),在直角坐标系XOY 中,X 轴上的动点M(x,0)到定点P(5,5)和到Q(2,1)的距离分别为MP 和MQ,那么当MP+MQ 取最小值时,点M 的横坐标x=__________________。 解:如图(2),只要画出点Q 关于x轴的对称点Q1(2,-1),连结PQ1 交x轴于点M,则M 点即为所求。点M 的横坐标只要先求出经过PQ1 两点的直线的解析式,(y=2x-5),令y=0,求得x=5/2。(也可以用勾股定理或相似三角形求出答案)。 3、 求函数y=2610xx +2634xx的最小值。 解:方法(Ⅰ) LPA1ACBDH(5,5)(2,1)YXOQP123456-1-1123456(5,5)(2,1)YXMOQPQ1123456-1-1123456图(1) 图(2) 图(1) 把原函数转化为y=1)3(2 x +22(3)5x ,因此可以理解为在X 轴上找一个点,使它到点(3,1)和(-3,5)的距离之和最小...