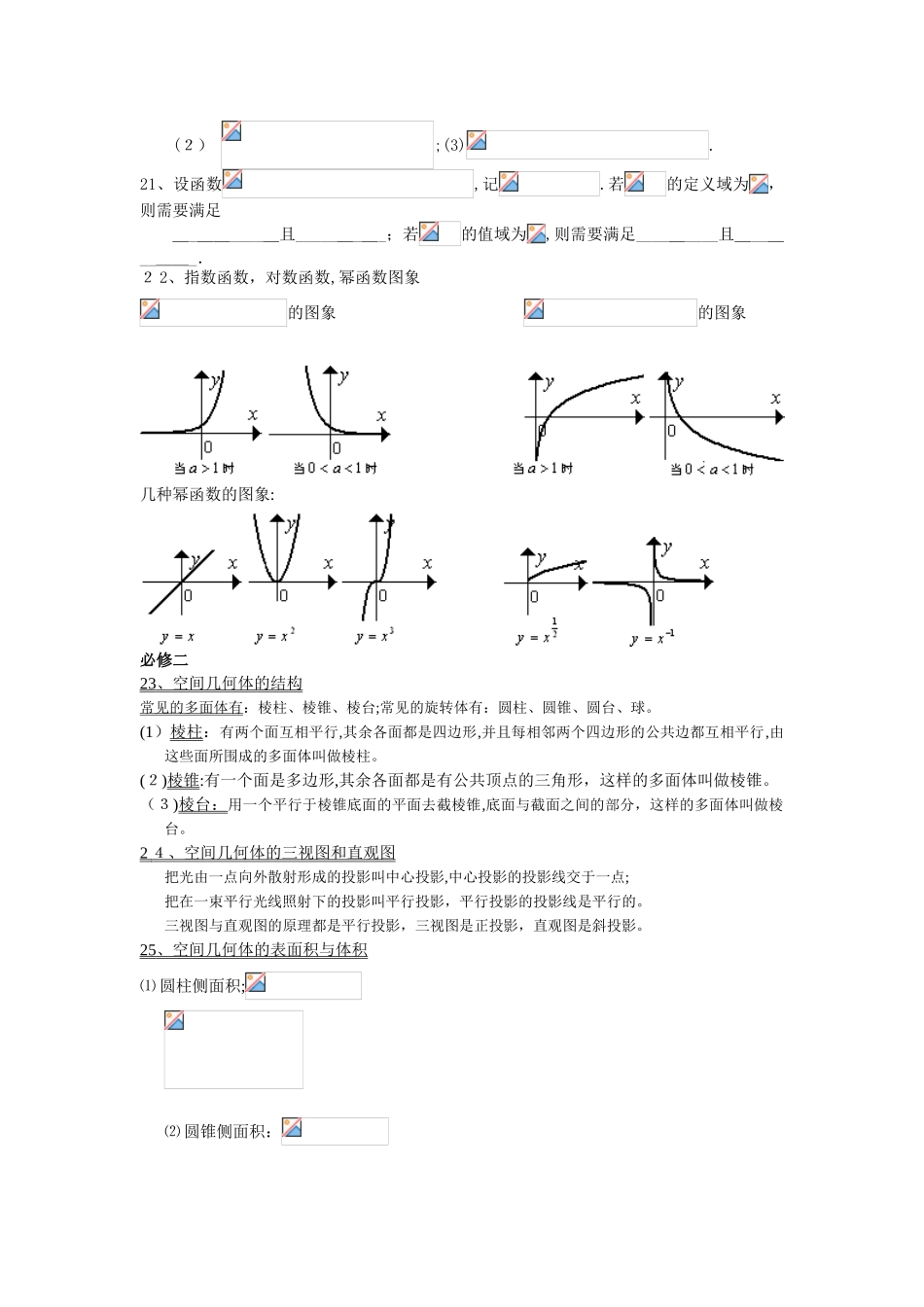
必修模块基础知识必修一1、德摩根定律:2、3、若A={},则A的子集有______个,真子集有______个,非空真子集有__________个.4、二次函数的解析式的三种形式①一般式________________;②顶点式________________;③零点式________________.5、二次函数,对称轴为________,顶点坐标为_________.6、二次函数,当时,值域为________;当时,值域为_______.7、二次函数在区间上的最值问题,①若,则_____________;_____________;②若h,则_____________;_____________;③若,则_____________;_____________;8、设一元二次方程的两个根为,则_________,_________。9、在区间上是增(减)函数当时();10、函数对定义域内的任意,若有_______________(其中为非零常数),则称函数为周期函数。11、函数对定义域内的任意,若有_______________,则称函数为奇函数;函数对定义域内的任意,若有_______________,则称函数为偶函数。12、奇函数的图象关于_________对称,在关于原点的对称区间上单调性___________,如果在原点有定义,则一定有___________________.13、偶函数的图象关于_________对称,在关于原点的对称区间上单调性___________。14、对于函数(),恒成立,则函数的对称轴是___________。15、对于函数(),恒成立,则函数的周期是___________;对于函数(),恒成立,则函数的周期是___________;对于函数(),恒成立,则函数的周期是___________;对于函数(),恒成立,则函数的周期是___________;16、分数指数幂化成根式:(,且).(,且)17、幂的运算律:(1).(2).(3)18、指数式与对数式的互化式19、对数的换底公式(,且,,且,).20、对数的四则运算法则(1);(2);(3).21、设函数,记.若的定义域为,则需要满足_________且_________;若的值域为,则需要满足_________且_________.22、指数函数,对数函数,幂函数图象的图象的图象几种幂函数的图象:必修二23、空间几何体的结构常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。(1)棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。(2)棱锥:有一个面是多边形,其余各面都是有公共顶点的三角形,这样的多面体叫做棱锥。(3)棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。24、空间几何体的三视图和直观图把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的。三视图与直观图的原理都是平行投影,三视图是正投影,直观图是斜投影。25、空间几何体的表面积与体积⑴圆柱侧面积;⑵圆锥侧面积:⑶圆台侧面积:⑷体积公式:;;⑸球的表面积和体积:.第二章:点、直线、平面之间的位置关系26、公理1:如果一条直线上两点在一个平面内,那么这条直线在此平面内。公理2:过不在一条直线上的三点,有且只有一个平面。公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。公理4:平行于同一条直线的两条直线平行.27、定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。28、线线位置关系:平行、相交、异面。29、线面位置关系:直线在平面内、直线和平面平行、直线和平面相交。30、面面位置关系:平行、相交。31、线面平行:⑴判定:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。⑵性质:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。32、面面平行:⑴判定:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。⑵性质:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。33、线面垂直:⑴定义:如果一条直线垂直于一个平面内的任意一条直线,那么就说这条直线和这个平面垂直。⑵判定:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。⑶性质:垂直于同一个平面的两条直线平行。3...