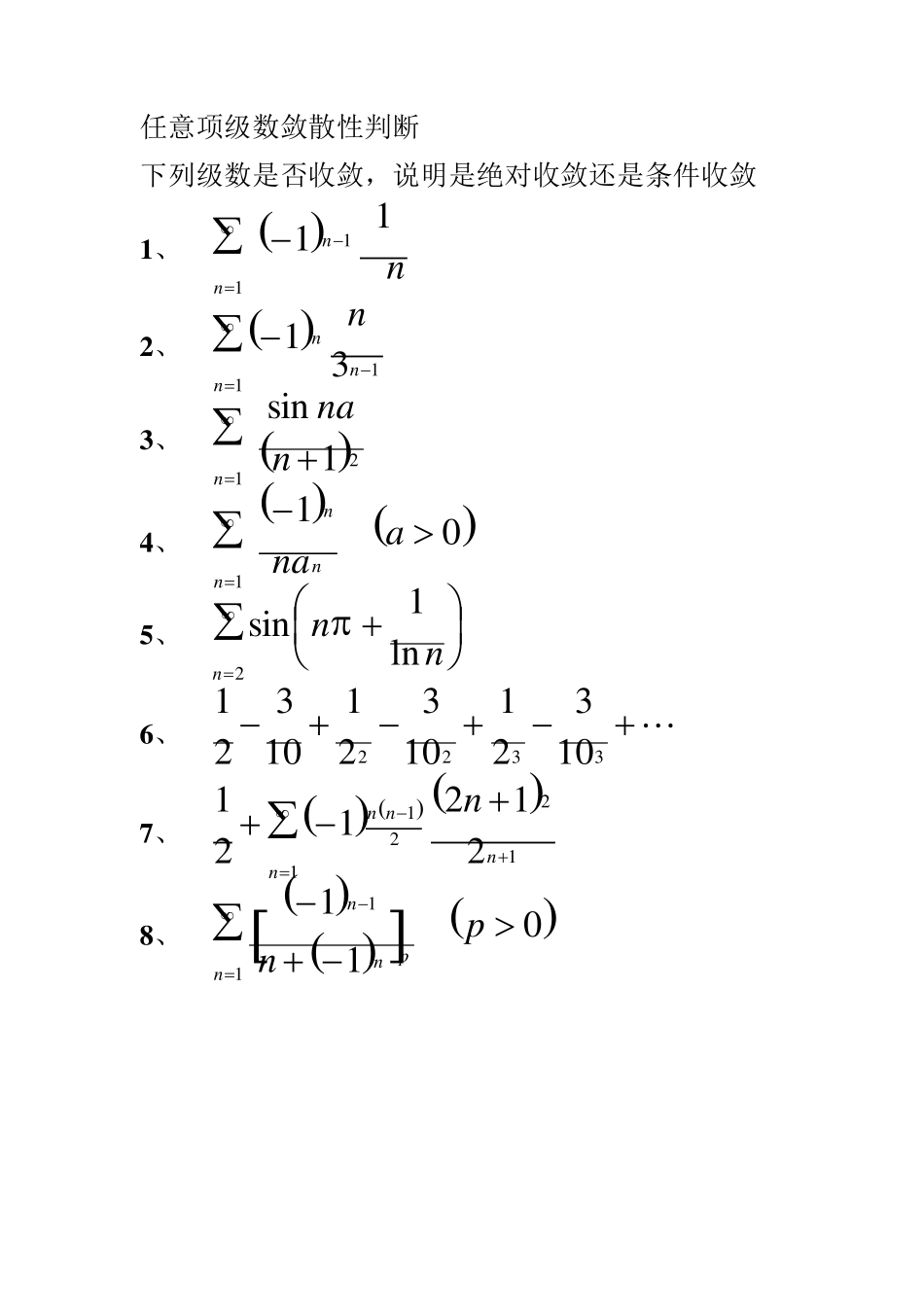任意项级数敛散性判断练习及答案

任意项级数敛散性判断 下列级数是否收敛，说明是绝对收敛还是条件收敛 1 、 11 11nnn 2 、 1131nnn n 3 、 121sinnnna 4 、  011anannn 5 、 2ln1sinnnn 6 、 3322103211032110321 7 、    11221212121nnnnn 8 、 01111pnnpnn 答 解：1、11 11nnn 取绝对值   11111nnnnn >∞ （ 21p 的 p 级数） 而原级数是交错级数 且： 01lim1111nunnunnn 由莱布尼兹定理，原级数收敛。所以是条件收敛。 2、1131nnn n 13111lim31331limlim11 nnnuunnnnnnn 绝对值级数  1131nnn n 所以原级数绝对收敛 3、121sinnnna 22111sinnnna 1211nn 是 p=2 的 p 级数。收敛！ 所以由比较判别法，原级数绝对收敛 4、 011anannn 111limlim11aannauunnnnn a>1 时原级数绝对收敛 01 原级数绝对收敛 p≦1 原级数发散