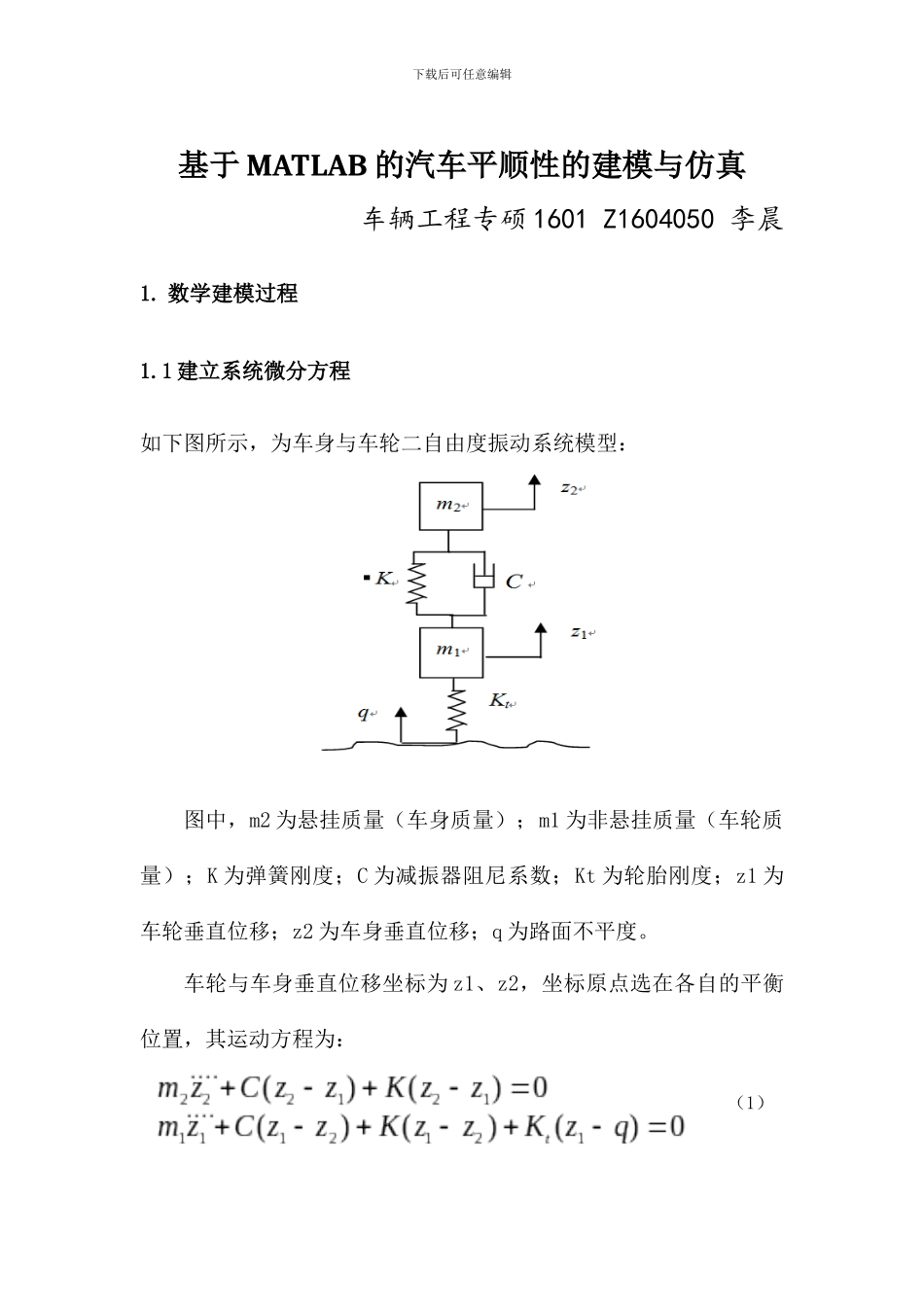
(1)下载后可任意编辑基于 MATLAB 的汽车平顺性的建模与仿真车辆工程专硕 1601 Z1604050 李晨1. 数学建模过程1.1 建立系统微分方程如下图所示,为车身与车轮二自由度振动系统模型:图中,m2 为悬挂质量(车身质量);m1 为非悬挂质量(车轮质量);K 为弹簧刚度;C 为减振器阻尼系数;Kt 为轮胎刚度;z1 为车轮垂直位移;z2 为车身垂直位移;q 为路面不平度。车轮与车身垂直位移坐标为 z1、z2,坐标原点选在各自的平衡位置,其运动方程为: (6)(2)(3)(4)(5)下载后可任意编辑1.2 双质量系统的传递特性先求双质量系统的频率响应函数,将有关各复振幅代入,得:令: 由式(2)得 z2-z1的频率响应函数: 将式(4)代入式(3)得 z1-q 的频率响应函数:式中:下面综合分析车身与车轮双质量系统的传递特性。车身位移 z2对路面位移 q 的频率响应函数,由式(4)及(5)两个环节的频率响应函数相乘得到:NKAAAAKAqztt2212321=-=(6)(11)(8)(9)(10)(7)下载后可任意编辑1.3 车身加速度、悬架弹簧动挠度和车轮相对动载的幅频特性1.车身加速度对路面不平度的频率特性:2.相对动载对路面不平度的频率特性车轮动载荷为: 车轮静载荷为:则车轮与路面相对动载为:车轮与路面间相对动载与路面不平度之间的传递函数为: 3.悬架动挠度对路面不平度的频率特性(13)(12)下载后可任意编辑悬架动挠度为:悬架动挠度与路面不平度之间的传递函数为: 2. 仿真过程通过建模,我们已经得到了各所需的传递函数。下面要利用MATLAB 的 M 文件进行仿真。2.1 公式的进一步推导在公式(7)中,我们需要得到的是传递函数的分子和分母表达式,这样可以通过插值的方法计算传递函数,并以此计算出幅频特性。经进一步推导后我们可得公式(7)的分子为: 分母为:下载后可任意编辑同理,对公式(11)、(13)进行推导得:公式(11)分子为: 分母为: 公式(13)分子为:分母为:2.2M 文件中代码的编写得到了所有传递函数的分子、分母,下面编写代码:1.一些系统参数的输入下载后可任意编辑2.传递函数分子、分母的构建3.传递响应函数的构建及频响输出车身加速度对路面不平度响应特性:下载后可任意编辑悬架动挠度对路面不平度响应特性:相对动载对路面不平度响应特性:2.3 图形输出下载后可任意编辑对比汽车理论教材上的内容,作出的曲线基本符合。