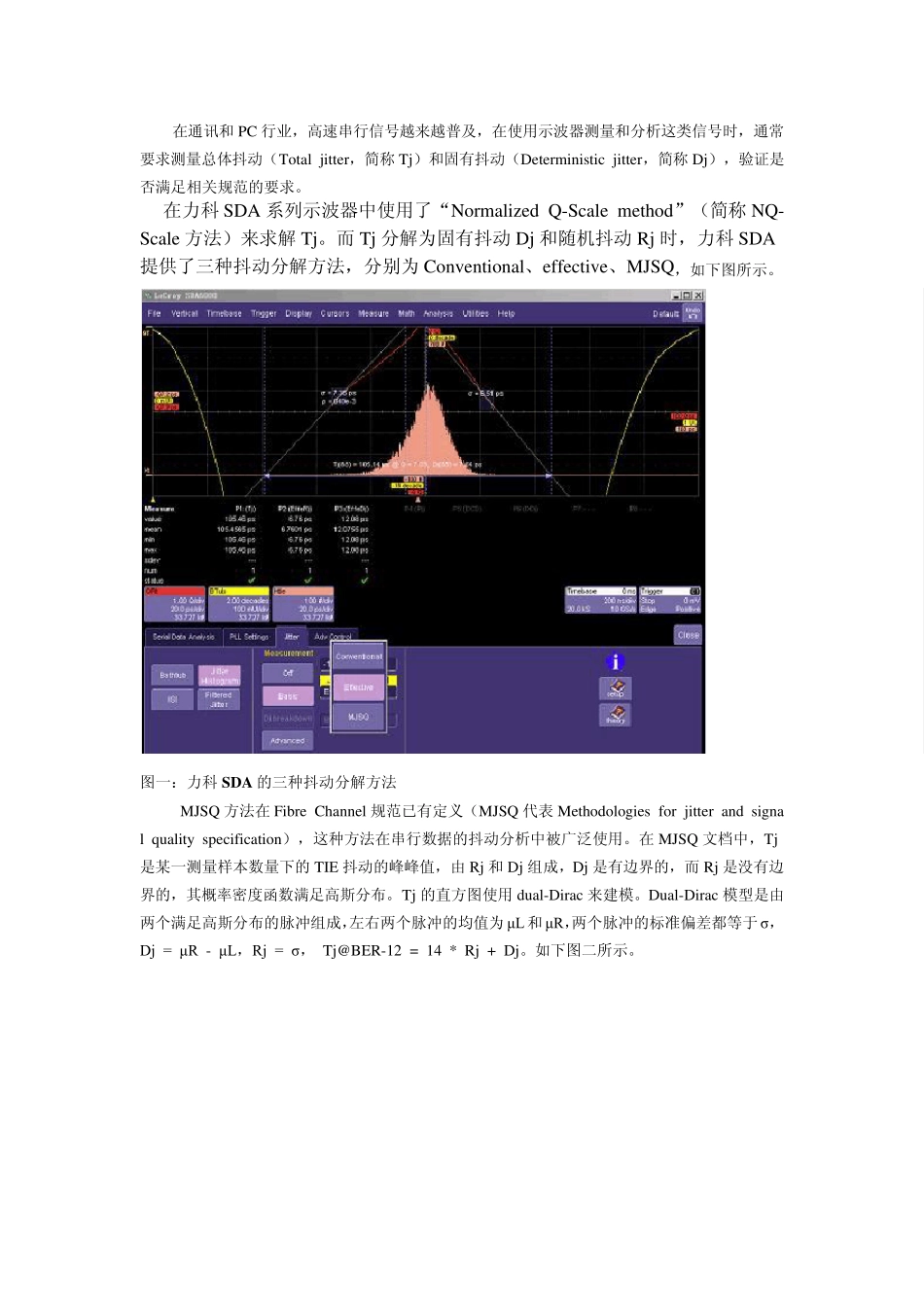
在通讯和PC 行业,高速串行信号越来越普及,在使用示波器测量和分析这类信号时,通常要求测量总体抖动(Total jitter,简称Tj)和固有抖动(Deterministic jitter,简称Dj),验证是否满足相关规范的要求。 在力科SDA 系列示波器中使用了“Normalized Q-Scale method”(简称NQ-Scale 方法)来求解 Tj。而 Tj 分解为固有抖动Dj 和随机抖动Rj 时,力科SDA提供了三种抖动分解方法,分别为 Conventional、effective、MJSQ,如下图所示。 图一:力科SDA 的三种抖动分解方法 MJSQ 方法在Fibre Channel 规范已有定义(MJSQ 代表 Methodologies for jitter and signal quality specification),这种方法在串行数据的抖动分析中被广泛使用。在MJSQ 文档中,Tj是某一测量样本数量下的TIE 抖动的峰峰值,由 Rj 和Dj 组成,Dj 是有边界的,而 Rj 是没有边界的,其概率密度函数满足高斯分布。Tj 的直方图使用dual-Dirac 来建模。Dual-Dirac 模型是由两个满足高斯分布的脉冲组成,左右两个脉冲的均值为 μL 和μR,两个脉冲的标准偏差都等于 σ,Dj = μR - μL,Rj = σ, Tj@BER-12 = 14 * Rj + Dj。如下图二所示。 图二:Dual-driac 模型与MJSQ 方法示意图 力科SDA 中的MJSQ 方法直接处理PDF 概率密度函数,使用两个高斯分布的曲线分别拟合TIE 直方图的左右两边的尾部,调节高斯曲线的标准偏差让曲线能尽量拟合TIE 直方图的尾部。 力科SDA 的MJSQ 分解方法基于传统的MJSQ 方法进行了革新,两个高斯分布的均值可以是不以Y 轴对称的,标准偏差也可以是不相等的。拟合的两个高斯曲线的均值之差为Dj,标准偏差的平均值为Rj。 Effectiv e方法是直接对浴盆曲线(bathtu b cu rv e)进行分析,将Tj 分解为Dj 和Rj。这种方法与误码率测试仪(BERT)的方法相同。在使用NQ-Scale 方法得到不同BER 下的Tj 后,由于Tj = Dj + α ×Rj,在不同BER 下的系数α 是已知,可以推算出不同BER 下的Dj 和Rj。如右图所示,BER=10e-12 时 α =14.069,BER=10e-10 时 α =12.723。 由于effectiv e 方法求解Dj 和Rj 与BERT 相似,所以使用这种方法的计算结果可以与BERT 的进行对比。另外,effectiv e 方法求解的Dj 和Rj 与MJSQ 方法的非常相似。 图三:力科SDA 中effectiv e 方法分解Tj Conventional 方法先计算Dj 中的周期性抖动Pj(periodic jitter)、数据...