信息光学习题答案

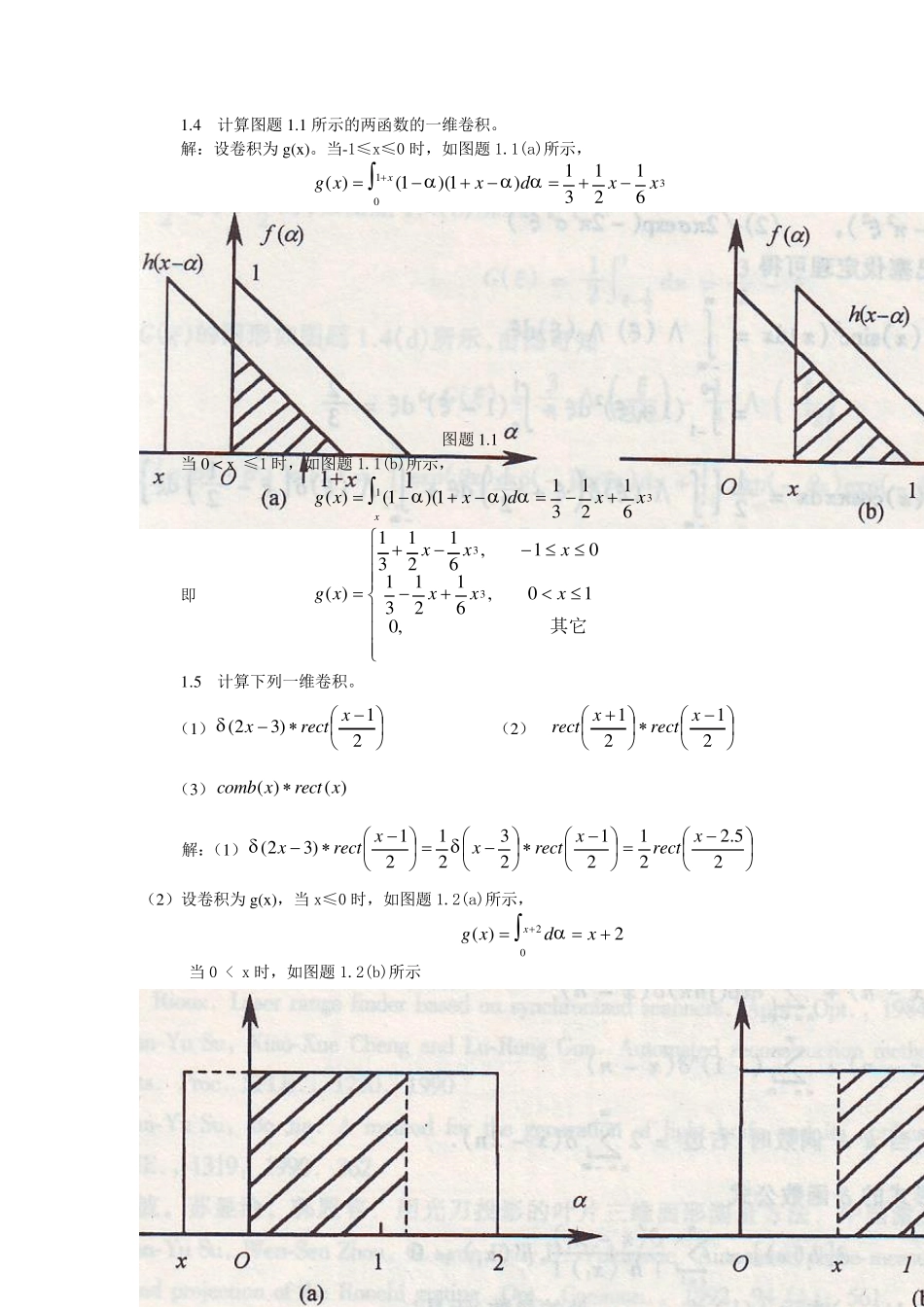
1 信息光学习题答案 第一章 线性系统分析 1.1 简要说明以下系统是否有线性和平移不变性. （1）  ;xfdxdxg （2）  ;dxxfxg （3）   ;xfxg （4）   ;2dxhfxg （5）  djf 2exp 解：（1）线性、平移不变； （2）线性、平移不变； （3）非线性、平移不变； （4）线性、平移不变； （5）线性、非平移不变。 1.2 证明)()exp()(2xcombxjxcombxcomb 证明：左边＝nnnnxnxnxxcomb)2(2)2(2122 nnnnnnnnxnxnxjnnxnxxjnxxjxcombxcomb)()1()()()exp()()()exp()()exp()()(右边 当 n 为奇数时，右边＝0，当 n 为偶数时，右边＝ nnx)2(2 所以当 n 为偶数时，左右两边相等。 1.3 证明)()(sinxcombx  证明：根据复合函数形式的 δ 函数公式 0)(,)()()]([1 iniiixhxhxxxh 式中ix 是h(x)=0 的根，)(ixh表示)(xh在ixx 处的导数。于是 )()()(sinxcombnxxn 2 1.4 计算图题1.1 所示的两函数的一维卷积。 解：设卷积为g(x)。当-1≤x≤0 时，如图题1.1(a)所示，  xxxdxxg103612131)1)(1()( 图题1.1 当0 < x ≤1 时，如图题1.1(b)所示， 13612131)1)(1()(xxxdxxg 即 其它,010,61213101,612131)(33xxxxxxxg 1.5 计算下列一维卷积。 （1）21)32(xrectx （2）2121xrectxrect （3）)()(xrectxcomb 解：（1）25.22121232121)32(xrectxrectxxrectx （2）设卷积为g(x)，当x≤0 时，如图题1.2(a)所示， 2)(20  xdxgx 当0 < x 时，如图题1.2(b)所示 3 图题1.2 xdxgx 2)(2  0,210,212)(xxxxxg 即 22)(xxg （3）1)()(xrectxcomb 1.6 已知)exp(2x的傅立叶变换为)exp(2，试求 （1）...