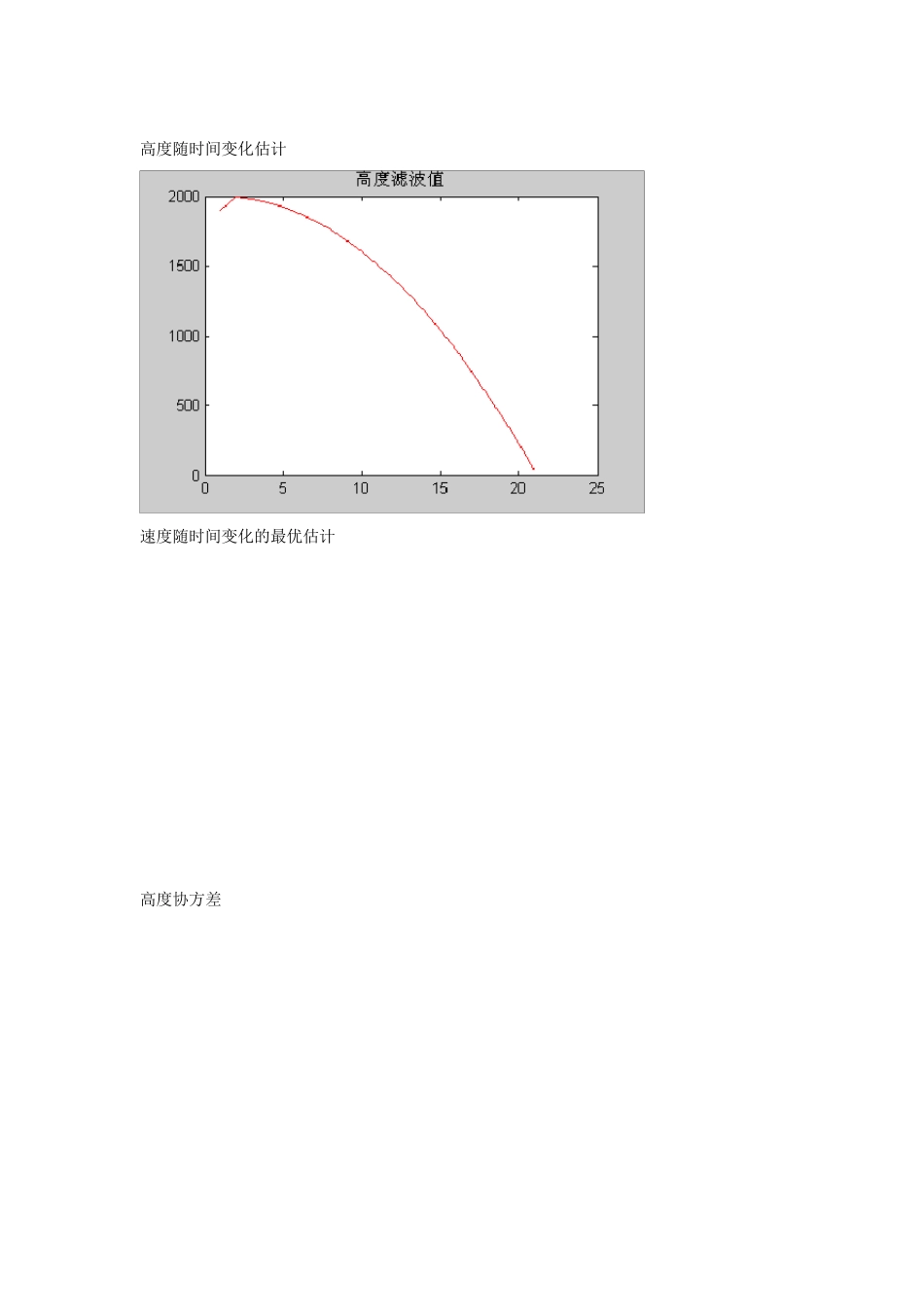
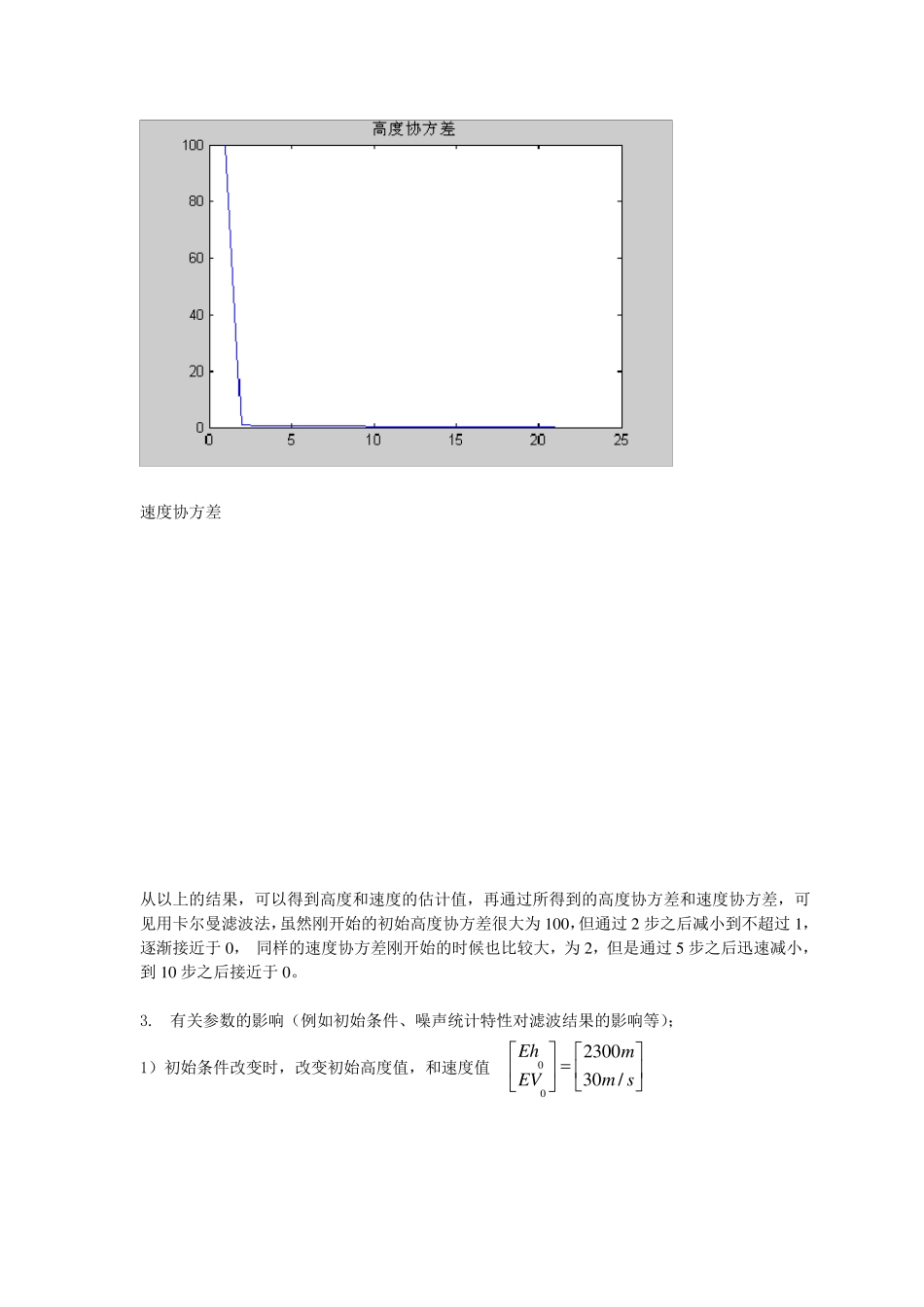
一. 已知一物体作自由落体运动,对其高度进行了20 次测量,测量值如下表: 时间[s] 1 2 3 4 5 6 7 高度[km] 1.9945 1.9794 1.9554 1.9214 1.8777 1.8250 1.7598 时间[s] 8 9 10 11 12 13 14 高度[km] 1.6867 1.6036 1.5092 1.4076 1.2944 1.1724 1.0399 时间[s] 15 16 17 18 19 20 高度[km] 0.8980 0.7455 0.5850 0.4125 0.2318 0.0399 设高度的测量误差是均值为0、方差为1 的高斯白噪声随机序列,该物体的初始高度0h 和速度0V也是高斯分布的随机变量,且0000019001000,var10/02EhhmPEVm sV。试求该物体高度和速度随时间变化的最优估计。(2/80.9smg ) 解: 1. 令( )( )( )h kX kv k t=1 R(k)=1 Q(k)=0 根据离散时间卡尔曼滤波公式,则有: (1)(1, )( )( )X kkk X kU k (1)(1)(1)(1)Y kH kX kV k (1, )kk= 11t ( )U k = 20.5 gtgt (1)H k =10 滤波初值:^1900(0 |0)(0)10XEX 0100(0 |0)var[(0)]2PXP 一步预测:^^(1| )(1, )( | )( )X kkkk X k kU k (1| )(1, ) ( | )(1, )TP kkkk P k kkk 滤波增益:1(1)(1| )(1)[(1) (1| )(1)(1)]TTK kP kk HkH kP kk HkR k 滤波计算:^^^(1|1)(1| )(1)[ (1)(1)(1| )]X kkX kkK kY kH kX kk (1|1)[(1)(1)] (1| )P kkIK kH kP kk 2. 实验结果 高度随时间变化估计 速度随时间变化的最优估计 高度协方差 速度协方差 从以上的结果,可以得到高度和速度的估计值,再通过所得到的高度协方差和速度协方差,可见用卡尔曼滤波法,虽然刚开始的初始高度协方差很大为1 0 0 ,但通过2 步之后减小到不超过1 ,逐渐接近于0 , 同样的速度协方差刚开始的时候也比较大,为2 ,但是通过5 步之后迅速减小,到1 0 步之后接近于0 。 3. 有关参数的影响(例如初始条件、噪声统计特性对滤波结果的影响等); 1)初始条件改变时,改变初始高度值,和速度值 002 3 0 03 0/EhmEVm s 由实验结果分析可得 度滤波值和速度滤波值在开始几步接近初始值,协方...