卡尔曼滤波器第五章

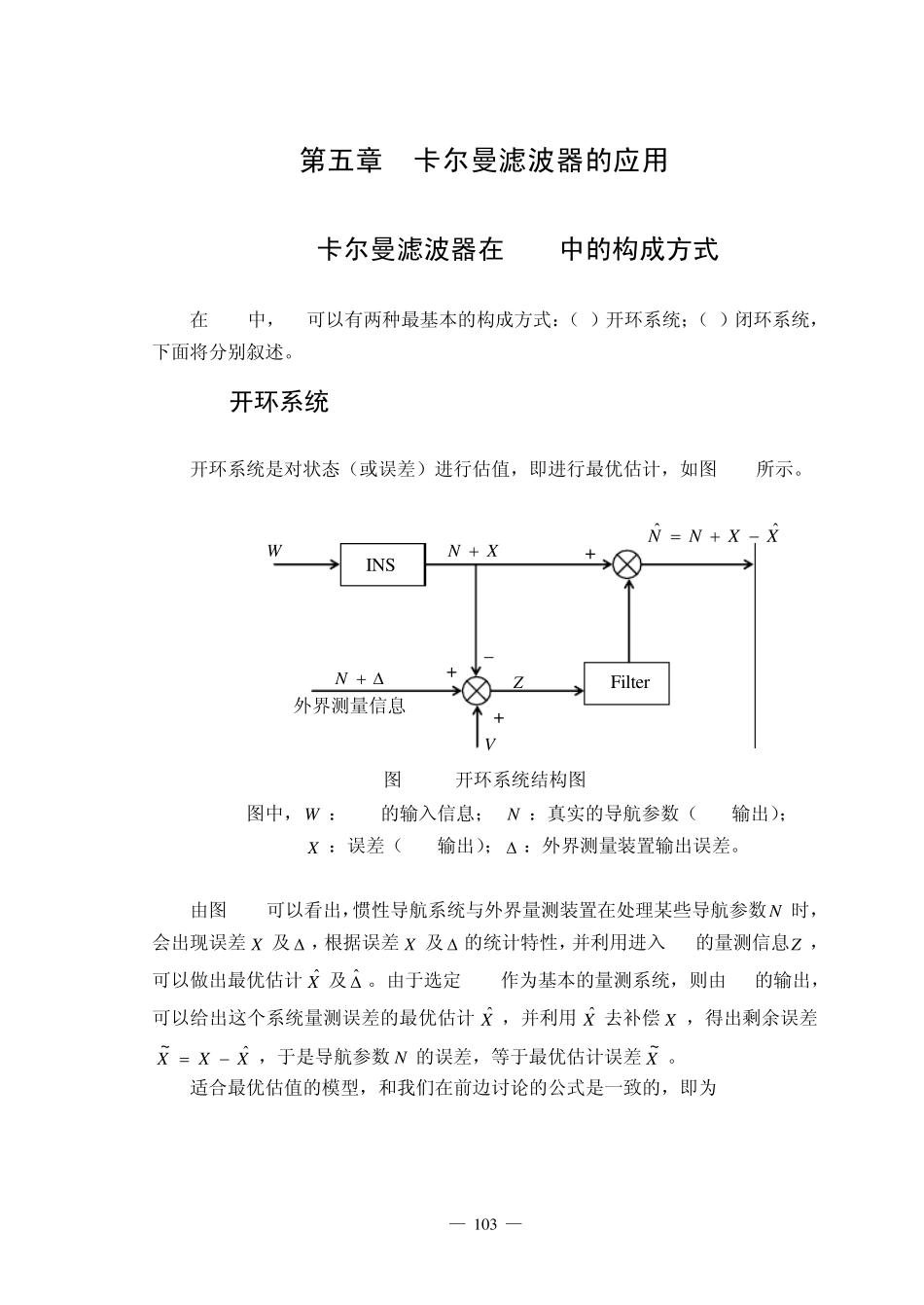
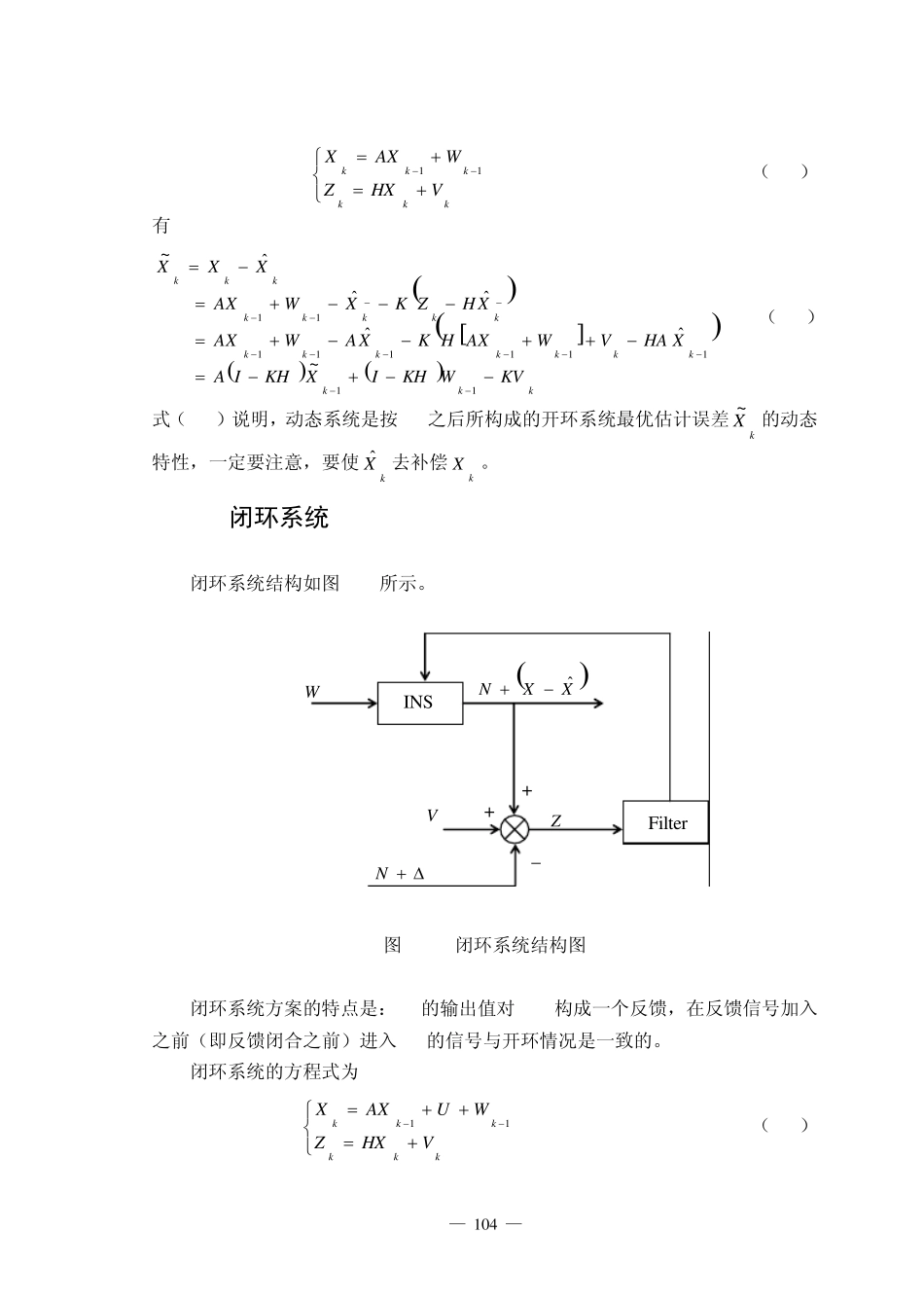
— 103 — 第五章 卡尔曼滤波器的应用 5.1 卡尔曼滤波器在INS中的构成方式 在 INS中，KF可以有两种最基本的构成方式：（1）开环系统；（2）闭环系统，下面将分别叙述。 5.1.1 开环系统 开环系统是对状态（或误差）进行估值，即进行最优估计，如图 5-1所示。 图 5-1 开环系统结构图 图中，W ：INS的输入信息； N ：真实的导航参数（INS输出）； X ：误差（INS输出）；  ：外界测量装置输出误差。 由图 5-1可以看出，惯性导航系统与外界量测装置在处理某些导航参数N 时，会出现误差 X 及  ，根据误差 X 及  的统计特性，并利用进入 KF的量测信息Z ，可以做出最优估计 Xˆ 及 ˆ 。由于选定 INS作为基本的量测系统，则由 KF的输出，可以给出这个系统量测误差的最优估计 Xˆ ，并利用 Xˆ 去补偿 X ，得出剩余误差XXXˆ~，于是导航参数 N 的误差，等于最优估计误差 X~ 。 适合最优估值的模型，和我们在前边讨论的公式是一致的，即为 INS Filter W XN  XXNNˆˆ N Z V _ + + + 外界测量信息 — 104 — kkkkkkVHXZWAXX11 （5-1） 有 kkkkkkkkkkkkkkkkkkKVWKHIXKHIAXHAVWAXHKXAWAXXHZKXWAXXXX1111111111~ˆˆˆˆˆ~ （5-2） 式（5-2）说明，动态系统是按 KF之后所构成的开环系统最优估计误差kX~的动态特性，一定要注意，要使kXˆ去补偿kX。 5.1.2 闭环系统 闭环系统结构如图 5-2所示。 图 5-2 闭环系统结构图 闭环系统方案的特点是：KF的输出值对 INS构成一个反馈，在反馈信号加入之前（即反馈闭合之前）进入 KF的信号与开环情况是一致的。 闭环系统的方程式为 kkkkkkVHXZWUAXX11 （5-3） INS Filter W XXNˆ N Z + + _ V — 105 — 在状态方程中，比（5-1）式多了一个控制项，它的 KF公式为： kkkkTkTkkkkkkkkkPHKIPRHHPHPKXHZKXXUXAXˆˆˆˆˆ1 (5-4) 这就是通常说的闭环系统 KF方程，和无控制输入的开环系统的 KF相比，除预测方程外，都是一样的。预测方程增加了一项控制输入U ，为了简单，U 取如下形式 KZU （5-5） 则系统动态方程为 kkkkkkkkkkKVWKHIXKHIAVHXKWAXKZWAXX...