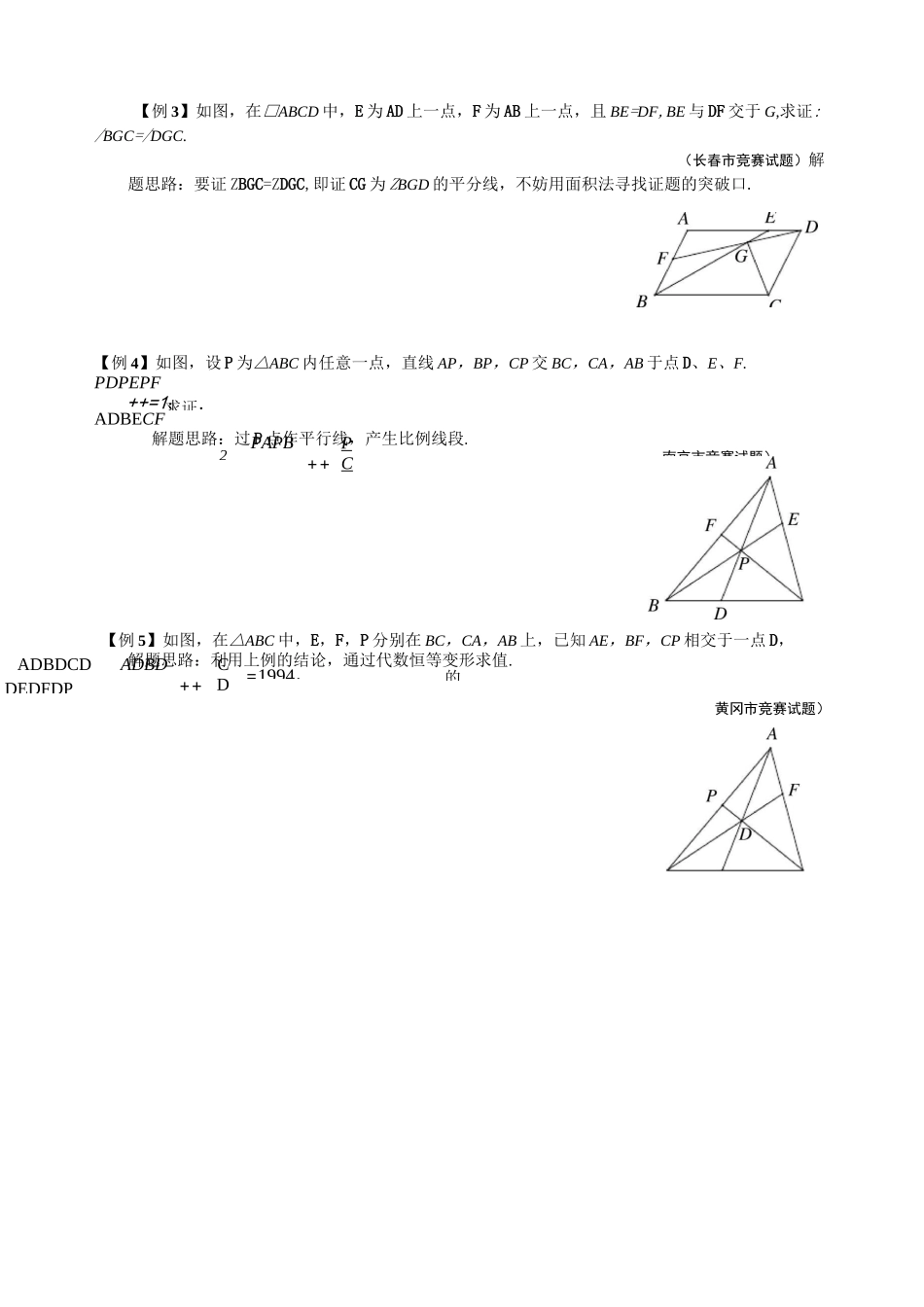
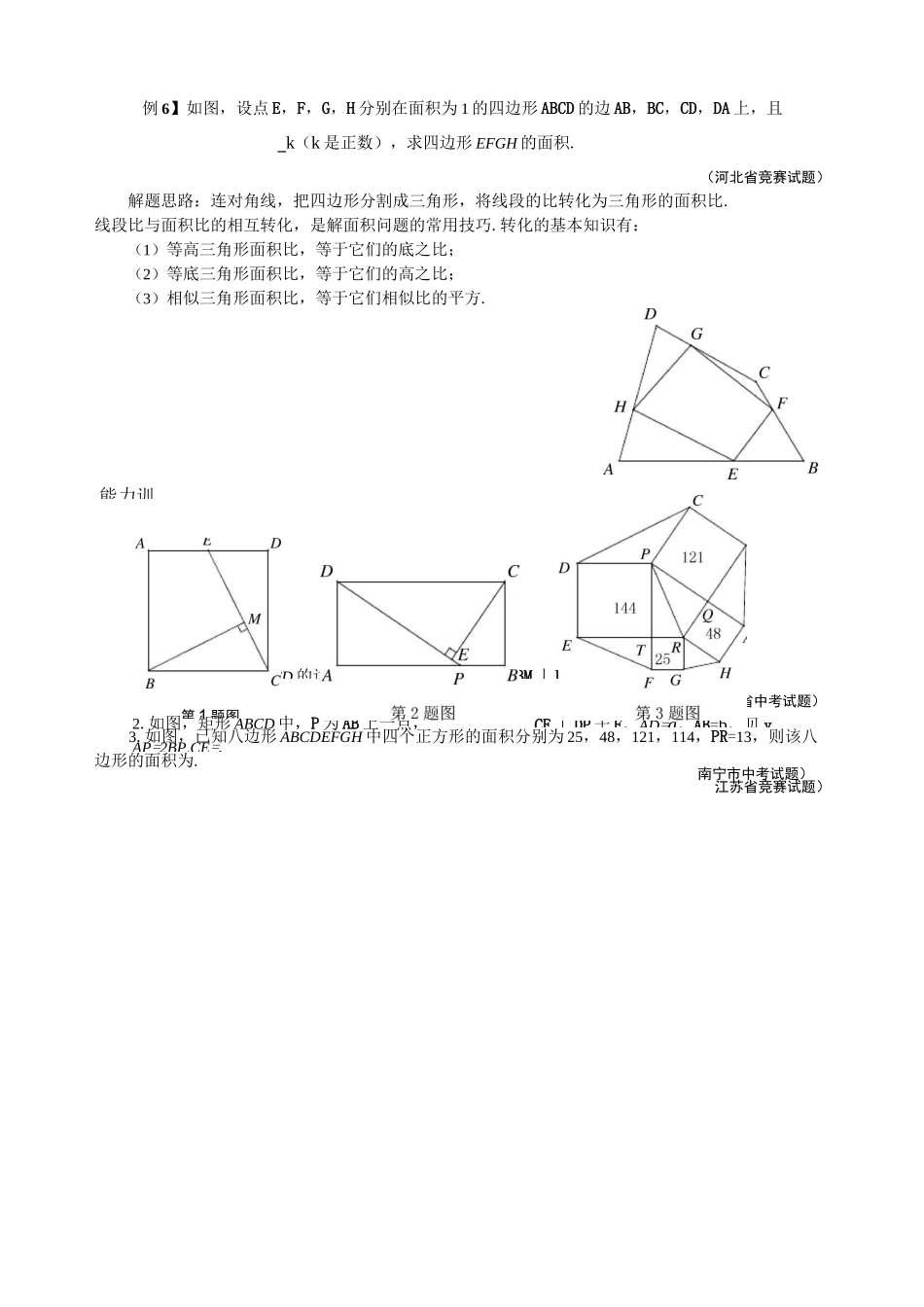
初中八年级数学培优训练(奥数)专题 27 面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要,面积关联着几何图形的重要元素边与角.所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法.有许多数学问题,虽然题目中没有直接涉及面积,但由于面积联系着几何图形的重要元素,所以借助于有关面积的知识求解,常常简捷明快.用面积法解题的基本思路是:对某一平面图形面积,采用不同方法或从不同角度去计算,就可得到一个含边或角的关系式,化简这个面积关系式就可得到求解或求证的结果.下列情况可以考虑用面积法:(1)涉及三角形的高、垂线等问题;(2)涉及角平分线的问题.例题与求解【例 1】如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为 1,3,5,则这个等边三角形的边长为.(全国初中数学联赛试题)解题思路:从寻求三条垂线段与等边三角形的高的关系入手.等腰三角形底边上任一点到两腰距离之和等于一腰上的高,那么等边三角形呢?等腰梯形呢?【例 2】如图,△AOB 中,ZO=9Oo,OA=OB,正方形 CDEF 的顶点 C 在 DA 上,点 D 在 OB2上,点 F 在 AB 上,如果正方形 CDEF 的面积是 AAOB 的面积的 5,则 OC:OD 等于()A.3:1B.2:1C.3:2D.5:3解题思路:由面积关系,可能想到边、角之间的关系,这时通过设元,即可把几何问题代数化来解决.求证:2PAPB++PC南京市竞赛试题)ADBD++CD=1994,ADBDCDDEDFDP的【例 3】如图,在□ABCD 中,E 为 AD 上一点,F 为 AB 上一点,且 BE=DF,BE 与 DF 交于 G,求证:/BGC=/DGC.(长春市竞赛试题)解题思路:要证 ZBGC=ZDGC,即证 CG 为 ZBGD 的平分线,不妨用面积法寻找证题的突破口.【例 4】如图,设 P 为△ABC 内任意一点,直线 AP,BP,CP 交 BC,CA,AB 于点 D、E、F.PDPEPF++=1;ADBECF解题思路:过 P 点作平行线,产生比例线段.【例 5】如图,在△ABC 中,E,F,P 分别在 BC,CA,AB 上,已知 AE,BF,CP 相交于一点 D,解题思路:利用上例的结论,通过代数恒等变形求值.黄冈市竞赛试题)能力训1.如图,正方形 ABCD 的边长为 4cm,E 是 AD 的中点,BM 丄 EC,垂足为 M,则 BM=2.如图,矩形 ABCD 中,P 为 AB 上一点,AP=2BP,CE=.(福建省中考试题)CE 丄 DP 于 E,AD=a,AB=b,贝 y南宁市中考试题)第 1 题图例 6】如图,设点 E,F,G,...