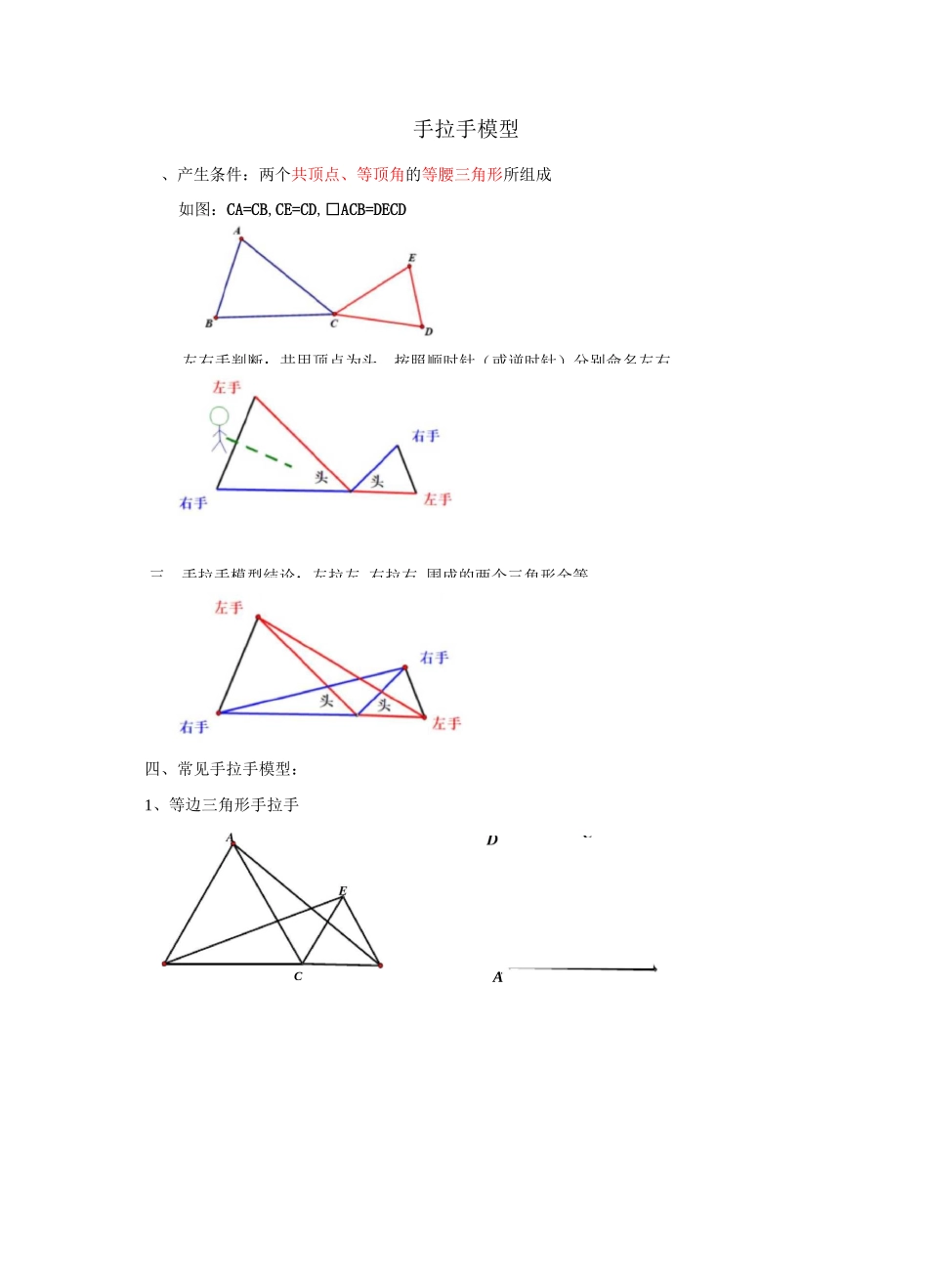
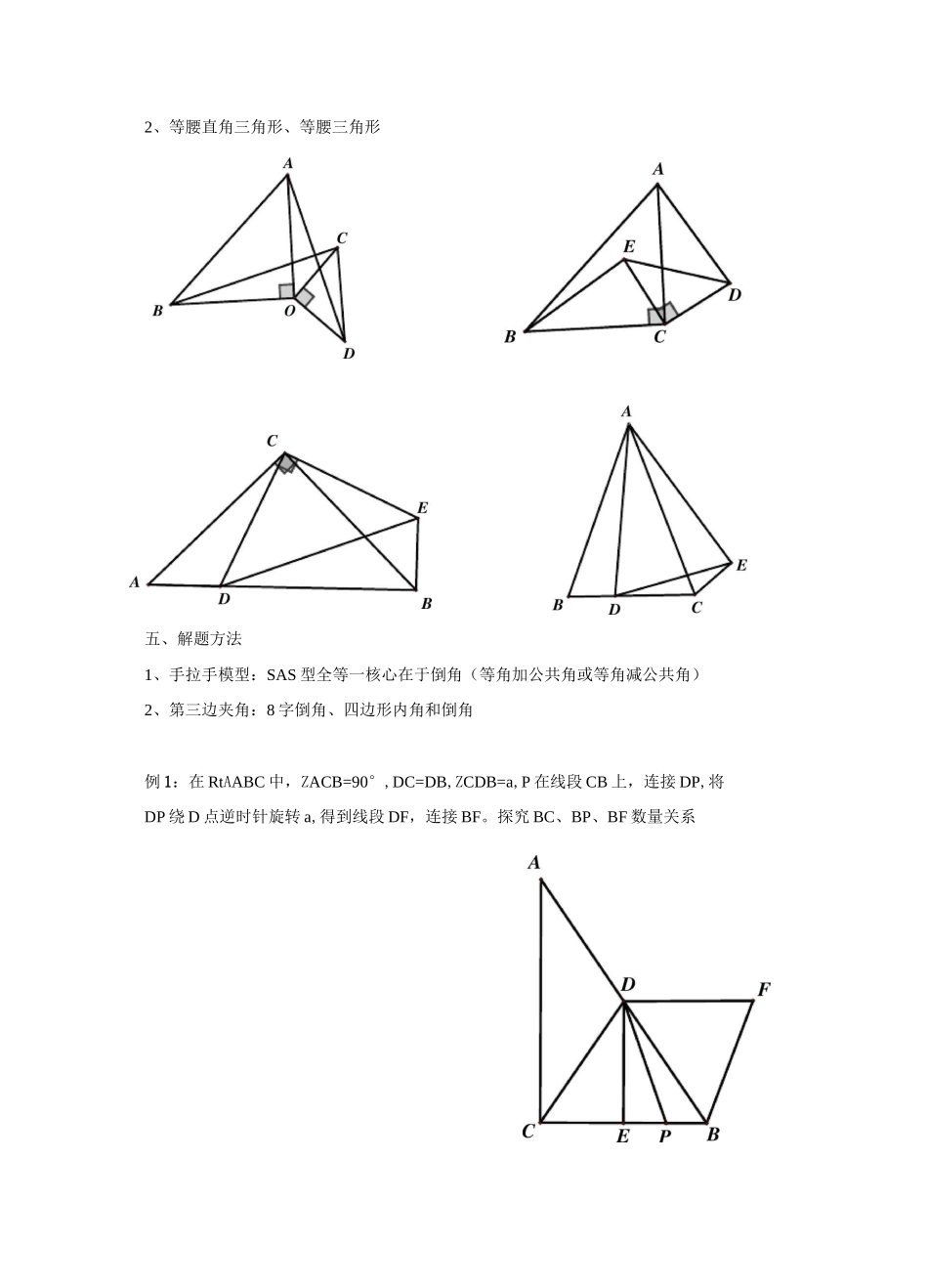
手拉手模型、产生条件:两个共顶点、等顶角的等腰三角形所组成如图:CA=CB,CE=CD,□ACB=DECD四、常见手拉手模型:1、等边三角形手拉手、左右手判断:共用顶点为头,按照顺时针(或逆时针)分别命名左右三、手拉手模型结论:左拉左,右拉右,围成的两个三角形全等CA2、等腰直角三角形、等腰三角形五、解题方法1、手拉手模型:SAS 型全等一核心在于倒角(等角加公共角或等角减公共角)2、第三边夹角:8 字倒角、四边形内角和倒角例 1:在 RtAABC 中,ZACB=90°,DC=DB,ZCDB=a,P 在线段 CB 上,连接 DP,将DP 绕 D 点逆时针旋转 a,得到线段 DF,连接 BF。探究 BC、BP、BF 数量关系(1) △ABE9△DBC(3)AE 与 CD 夹角为 60°(5)△BGE9△BFC(7)GF#AC(2) AE=DC(4)△AGE9△DFB(6)BH 平分 ZAHC(8)AH=DH+BH例 2.如图 AABD 与 ABCE 为等边三角形,ABC 三点共线,连结 AE 与 CD,证明:变式精练 1:如图,两个等边三角形 AABD 与 ABCE,连结 AE 与 CD,证明:(1) △ABE 今△DBC(2) AE=CD(3) AE 与 CD 的夹角(4) AE 与 CD 的交点为 H,求证 BH 平分 ZAHC变式精练 2:如图两个等边三角形 AABD 与 ABCE,连结 AE 与 CD,证明:(1) △ABE9△DBC(2) AE=CD(3) AE 与 CD 的夹角(4) AE 与 CD 的交点为 H,求证 BH 平分 ZAHC例 2:如图,两个等腰直角三角形 ADC 与 EDG,连结 AG,CE,二者相交于点 H,问:(1) △ADG9△CDE.(2) AG=CE(3) AG 与 CE 的夹角H0(4) BH 是否平分 ZAHE例 3:两个等腰三角形 AABD 与 ABCE,其中 AB=BD,CB=EB,ZABD=ZCBE=a,连结 AE 与 CD,问:(1) △ABE9△DBC(2) AE=CD(3) AE 与 CD 的夹角(4) BH 是否平分 ZAHC变式训练 1:在 AABC 中,AB=AC,点 D 是直线 BC 上一点(不与 B、C 重合),以 AD为一边在 AD 的右侧作厶 ADE,使 AD 二 AE,ZDAE=ZBAC,连接 CE.(1)如图 1,当点 D 在线段 BC 上,如果 ZBAC=90,则 ZBCE=度;(2)设 ZBAC=a,ZBCE 二 B.如图 2,当点 D 在线段 BC 上移动,则 a,P 之间有怎样的数量关系?请说明理由;例 4.如图,DABC 为等边三角形:(1) 如图 1,DEDBC,求证:DADE 是等边三角形(2) 如图 2,DADE 是等边三角形,点 B 在 ED 的延长线上,连接 CE,判断 DBEC 的度数及线段 AE、BE、CE 之间的数量关系。(3) 如图,DACB 和口 DCE 均为等腰直角三角形,DACB=DDCE=90°,点 A、D、E 在同一直线上,CM 为口 DCE 中 DE 边上的高,连接 BE.请判断 DAEB 的度数及线段 CM、