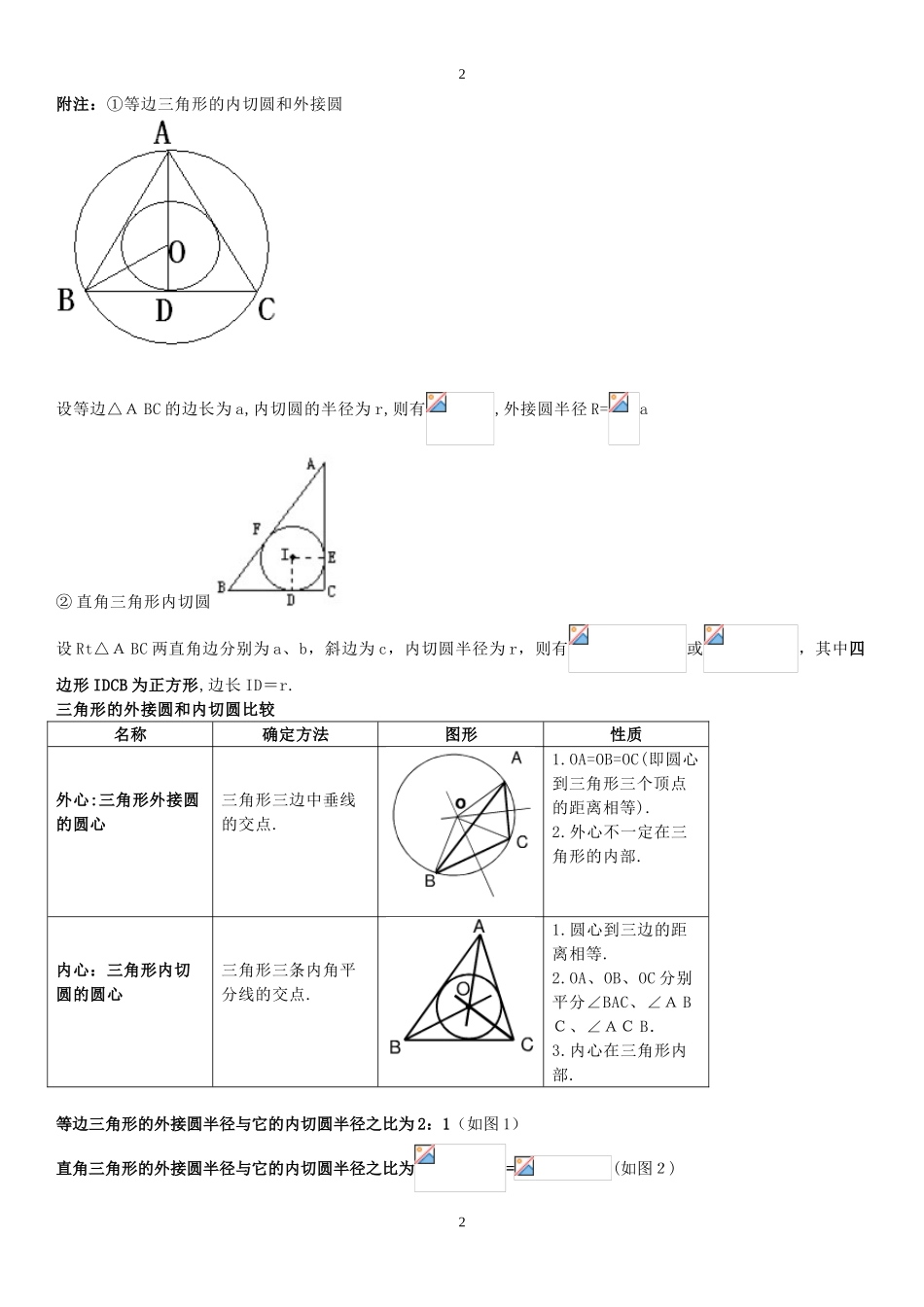
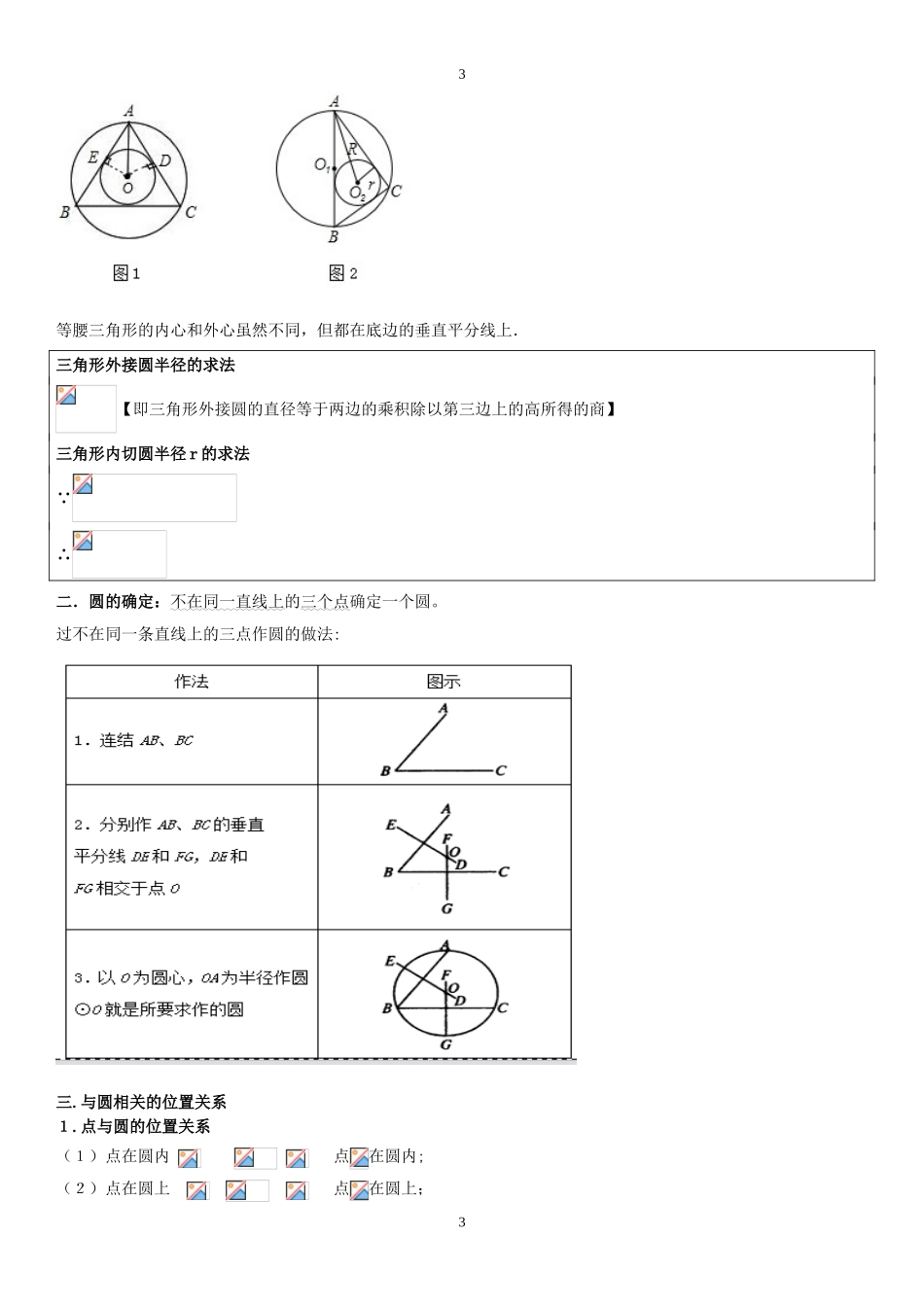
11第三章圆一.与圆相关的概念1.圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径.【圆心决定圆的位置,半径决定圆的大小,圆心和半径确定了,圆就确定了】2.①圆弧:圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧,等于半圆的弧叫半圆.②等弧:在同圆或等圆中,能够互相重合的弧叫等弧。等弧的长度相等,所含度数相等(即弯曲程度相等).等弧也可以通过它所对的圆心角、圆周角、弦来进行判断,具体地说:a.在同圆或等圆中,所对的圆心角相等的两段弧是等弧。b.在同圆或等圆中,所对的圆周角相等的两段弧是等弧。c.在同圆或等圆中,所对的弦相等的两段弧是等弧。【温馨提示:半圆是弧,半圆形不是弧;弧的度数等于弧所对的圆心角的度数.】3.弦:连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。圆中最长的弦是直径.【温馨提示:一条弦对着两条弧,对着两个圆心角(选择题),一般让求“弦所对的圆心角的度数”,指的是“弦所对的小于180°的那个圆心角”(填空题);一条弧对着一条弦,对着一个圆心角】4.圆心角:顶点在圆心上,角的两边与圆周相交的角叫圆心角.【圆心角∠AOB的取值范围是0°<∠AOB<360°】5.圆周角:顶点在圆周上,并且两边都和圆相交的角叫圆周角.6.外心:过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;这个三角形叫做圆的内接三角形.三角形外接圆的圆心(外心)到三角形三个顶点的距离相等.【温馨提示:三角形三边垂直平分线的交点叫三角形外接圆的圆心;三角形有且只有一个外接圆,但圆有无数个内接三角形】以下图为例O为外接圆的圆心,即外心.温馨提示:锐角三角形外接圆的圆心(外心)在它的内部;直角三角形外接圆的圆心(外心)在它斜边的中点上(R=);钝角三角形外接圆的圆心(外心)在它的外部.7.内心:和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为三角形的内心;这个三角形叫做圆的外切三角形.三角形内切圆的圆心(内心)到三角形三边的距离相等.【温馨提示:三角形三条角平分线的交点叫内切圆的圆心;三角形有且只有一个内切圆,但圆有无数个外切三角形】22附注:①等边三角形的内切圆和外接圆设等边△ABC的边长为a,内切圆的半径为r,则有,外接圆半径R=a②直角三角形内切圆设Rt△ABC两直角边分别为a、b,斜边为c,内切圆半径为r,则有或,其中四边形IDCB为正方形,边长ID=r.三角形的外接圆和内切圆比较名称确定方法图形性质外心:三角形外接圆的圆心三角形三边中垂线的交点.1.OA=OB=OC(即圆心到三角形三个顶点的距离相等).2.外心不一定在三角形的内部.内心:三角形内切圆的圆心三角形三条内角平分线的交点.1.圆心到三边的距离相等.2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB.3.内心在三角形内部.等边三角形的外接圆半径与它的内切圆半径之比为2:1(如图1)直角三角形的外接圆半径与它的内切圆半径之比为=(如图2)33等腰三角形的内心和外心虽然不同,但都在底边的垂直平分线上.三角形外接圆半径的求法【即三角形外接圆的直径等于两边的乘积除以第三边上的高所得的商】三角形内切圆半径r的求法 ∴二.圆的确定:不在同一直线上的三个点确定一个圆。过不在同一条直线上的三点作圆的做法:三.与圆相关的位置关系1.点与圆的位置关系(1)点在圆内点在圆内;(2)点在圆上点在圆上;44(3)点在圆外点在圆外;2.直线与圆的位置关系(1)直线与圆相离无交点;(2)直线与圆相切有一个交点;(3)直线与圆相交有两个交点;三.与圆相关的性质和定理1.圆的对称性:圆是轴对称图形,对称轴是任意一条经过圆心的直线(或直径所在的直线),它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.圆的旋转不变性:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.★★★2.垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。3.圆心角定理圆...