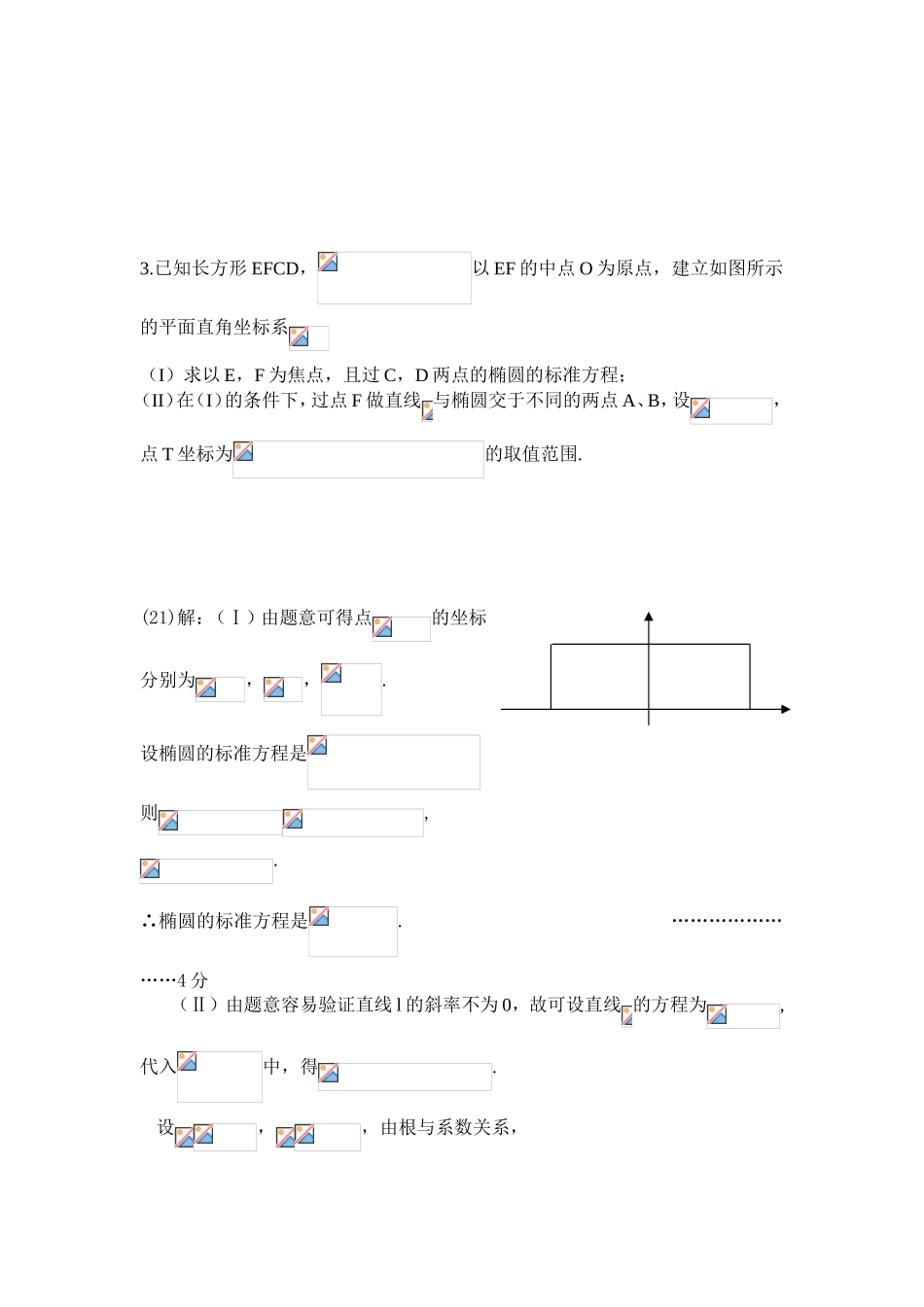
1.设F1,F2分别是双曲线的左、右焦点,若双曲线右支上存在一点P,使,O为坐标原点,且,则该双曲线的离心率为由得,即,所以,所以△PF1F2中,边F1F2上的中线等于|F1F2|的一半,可得,所以,又,解得,又,所以,所以双曲线的离心率为为.2.若双曲线渐近线上的一个动点P总在平面区域内,则实数的取值范围是.双曲线的渐近线为,即要使渐近线上的一个动点P总在平面区域内,则有圆心到渐近线的距离,即,解得,即或,所以则实数的取值范围是。3.已知长方形EFCD,以EF的中点O为原点,建立如图所示的平面直角坐标系(I)求以E,F为焦点,且过C,D两点的椭圆的标准方程;(II)在(I)的条件下,过点F做直线与椭圆交于不同的两点A、B,设,点T坐标为的取值范围.(21)解:(Ⅰ)由题意可得点的坐标分别为,,.设椭圆的标准方程是则,.∴椭圆的标准方程是.……………………4分(Ⅱ)由题意容易验证直线l的斜率不为0,故可设直线的方程为,代入中,得.设,,由根与系数关系,得=①,=②,……………………7分因为,所以且,所以将上式①的平方除以②,得,即=,所以=,由,即.又=,.故.…………………………………………………………11分令,因为,所以,,,因为,所以,.…………………………………………………………13分