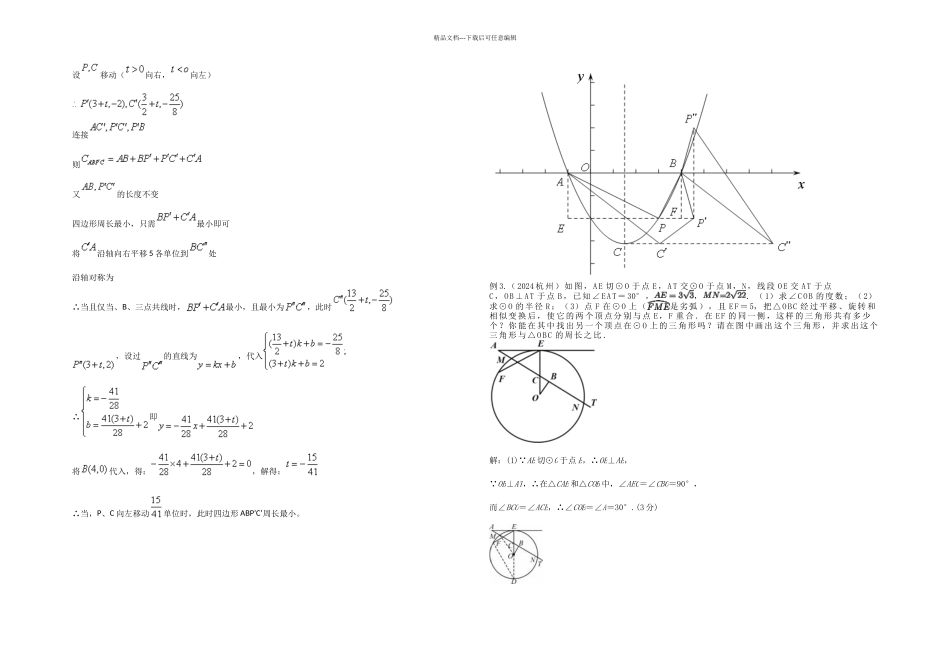
精品文档---下载后可任意编辑【中考热点分析】 数形结合思想是数学中重要的思想方法,它根据数学问题中的条件和结论之间的内在联系,既分析其数量关系,又揭示其几何意义,使数量关系和几何图形巧妙的结合起来,并充分利用这种结合,探求解决问题的思路,使问题得以解决的思考方法。几何图形的形象直观,便于理解;代数方法的一般性,解题过程的操作性强,便于把握。【经典考题讲练】例 1.(2024 衢州)如图,已知直线分别交 x 轴、y 轴于点 A、B,P 是抛物线的一个动点,其横坐标为 a,过点 P 且平行于 y 轴的直线交直线于点 Q,则当 PQ=BQ 时,a 的值是.例 2.(2024•广州)已知平面直角坐标系中两定点 A(-1,0),B(4,0),抛物线()过点 A、B,顶点为 C.点 P(m,n)(n<0)为抛物线上一点.(1)求抛物线的解析式与顶点 C 的坐标.(2)当∠APB 为钝角时,求 m 的取值范围.(3)若,当∠APB 为直角时,将该抛物线向左或向右平移 t()个单位,点 P、C 移动后对应的点分别记为、,是否存在 t,使得首尾依次连接 A、B、、所构成的多边形的周长最短?若存在,求 t值并说明抛物线平移的方向;若不存在,请说明理由.解析:(1)待定系数法求解析式即可,求得解析式后转换成顶点式即可.(2)因为 AB 为直径,所以当抛物线上的点 P 在⊙C 的内部时,满足∠APB 为钝角,所以-1<m<0,或 3<m<4.(3)左右平移时,使 A′D+DB″最短即可,那么作出点 C′关于 x 轴对称点的坐标为 C″,得到直线 P″C″的解析式,然后把 A 点的坐标代入即可.答案:(1)解:依题意把的坐标代入得: ;解得: 抛物线解析式为顶点横坐标,将代入抛物线得(2)如图,当时,设,则过作直线轴, (注意用整体代入法)解得,当在之间时,或时,为钝角.(3)依题意,且精品文档---下载后可任意编辑设移动(向右,向左)连接则又的长度不变四边形周长最小,只需最小即可将沿轴向右平移 5 各单位到处沿轴对称为∴当且仅当、B、三点共线时,最小,且最小为,此时,设过的直线为,代入∴即将代入,得:,解得:∴当,P、C 向左移动单位时,此时四边形 ABP’C’周长最小。例 3.(2024 杭州)如图,AE 切⊙O 于点 E,AT 交⊙O 于点 M,N,线段 OE 交 AT 于点C,OB⊥AT 于点 B,已知∠EAT=30°,,.(1)求∠COB 的度数;(2)求⊙O 的半径 R;(3)点 F 在⊙O 上(是劣弧),且 EF=5,把△OBC 经过平移、...