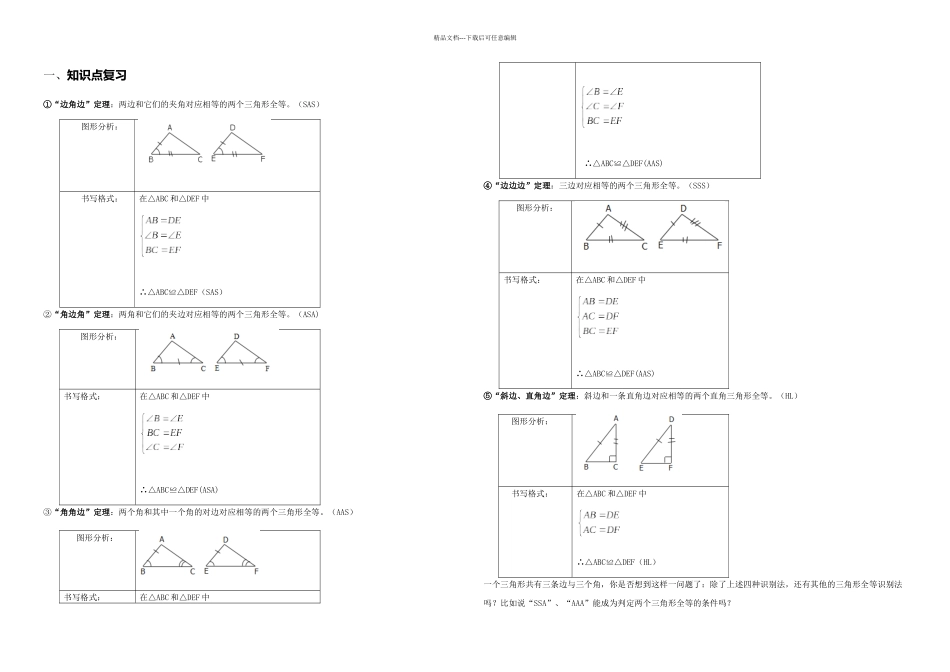
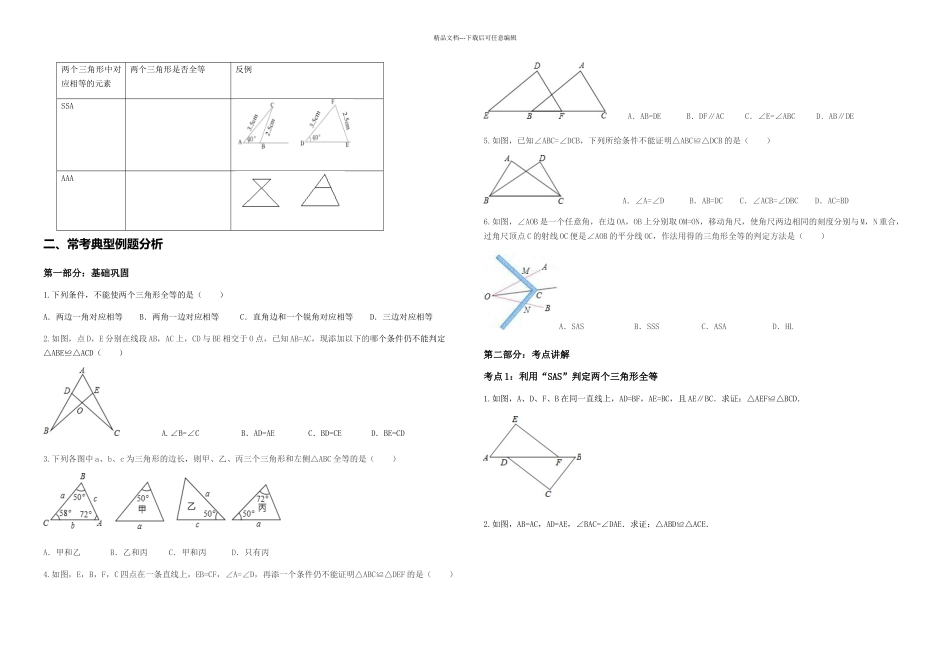
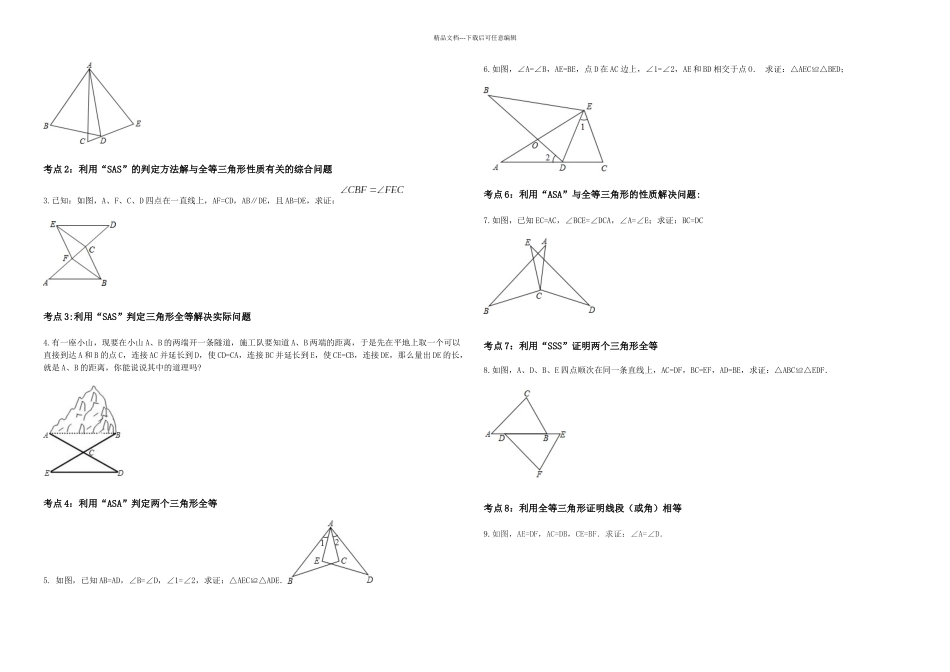
精品文档---下载后可任意编辑一、知识点复习①“边角边”定理:两边和它们的夹角对应相等的两个三角形全等。(SAS) 图形分析: 书写格式:在△ABC 和△DEF 中∴△ABC≌△DEF(SAS)②“角边角”定理:两角和它们的夹边对应相等的两个三角形全等。(ASA) 图形分析:书写格式:在△ABC 和△DEF 中∴△ABC≌△DEF(ASA)③“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等。(AAS) 图形分析:书写格式:在△ABC 和△DEF 中 ∴△ABC≌△DEF(AAS)④“边边边”定理:三边对应相等的两个三角形全等。(SSS) 图形分析:书写格式:在△ABC 和△DEF 中∴△ABC≌△DEF(AAS)⑤“斜边、直角边”定理:斜边和一条直角边对应相等的两个直角三角形全等。(HL) 图形分析:书写格式:在△ABC 和△DEF 中∴△ABC≌△DEF(HL)一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?精品文档---下载后可任意编辑两个三角形中对应相等的元素两个三角形是否全等反例SSAAAA二、常考典型例题分析 第一部分:基础巩固1.下列条件,不能使两个三角形全等的是( )A.两边一角对应相等 B.两角一边对应相等 C.直角边和一个锐角对应相等 D.三边对应相等2.如图,点 D,E 分别在线段 AB,AC 上,CD 与 BE 相交于 O 点,已知 AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( ) A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.下列各图中 a、b、c 为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC 全等的是( )A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙4.如图,E,B,F,C 四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF 的是( ) A.AB=DE B.DF∥AC C.∠E=∠ABC D.AB∥DE5.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB 的是( ) A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD6.如图,∠AOB 是一个任意角,在边 OA,OB 上分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与 M,N 重合,过角尺顶点 C 的射线 OC 便是∠AOB 的平分线 OC,作法用得的三角形全等的判定方法是( )A.SAS B.SSS C.ASA D.HL第二部分:考点讲解考点 1:利用“SAS”判定两个三角形全等1.如图,A、D、F、B 在同一直线上,AD=BF,AE=BC...