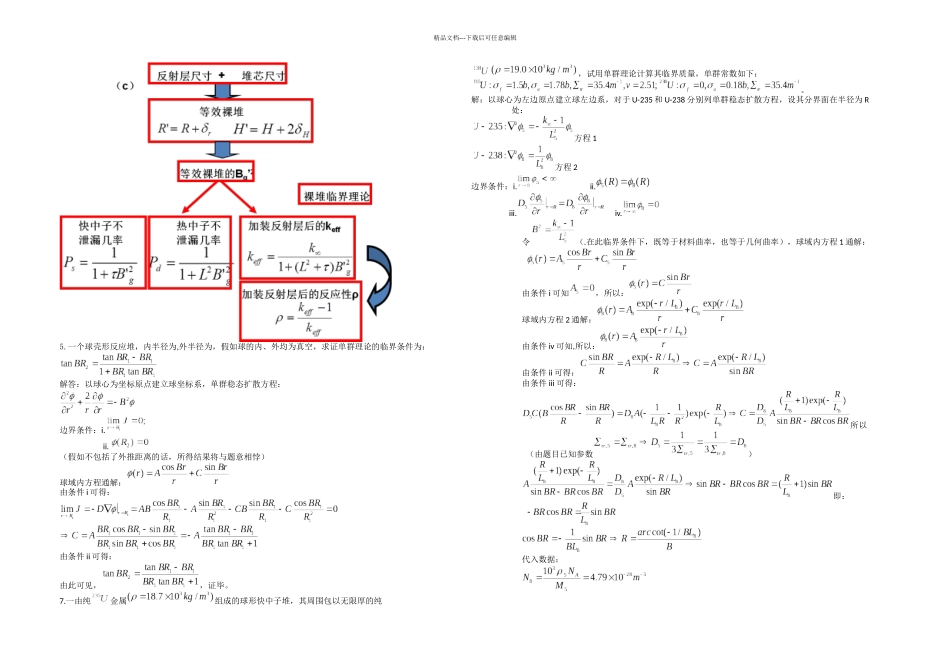
精品文档---下载后可任意编辑1.试求边长为(包括外推距离)的长方体裸堆的几何曲率和中子通量密度的分布。设有一边长(包括外推距离)的长方体裸堆,。(1)求达到临界时所必须的;(2)假如功率为,求中子通量密度分布。解:长方体的几何中心为原点建立坐标系,则单群稳态扩散方程为:边界条件:(以下解题过程都不再强调外推距离,可认为所有外边界尺寸已包含了外推距离)因为三个方向的通量拜年话是相互独立的,利用分离变量法:将方程化为:设:想考虑 X 方向,利用通解:代入边界条件:同理可得:其中是待定常数。其几何曲率:(1)应用修正单群理论,临界条件变为:其中:(2)只须求出通量表达式中的常系数2.设一重水—铀反应堆的堆芯。试按单群理论,修正单群理论的临界方程分别求出该芯部的材料曲率和达到临界时候的总的中子不泄露几率。解:对于单群理论:在临界条件下:(或用)对于单群修正理论:在临界条件下:(注意:这时能用,实际上在维持临界的前提条件下修正理论不会对不泄露几率产生影响,但此时的几何曲率、几何尺寸已发生了变化,不再是之前的系统了。)4.设有圆柱形铀-水栅装置,米,水位高度米,设栅格参数为:k∞,L2×10-4米 2,τ×10-2米 2。(a)试求该装置的有效增殖系数 k;(b)当该装置恰好达临界时,水位高度 H 等于多少?(c)设某压水堆以该铀-水栅格作为芯部,堆芯的尺寸为米,米,若反射层节约估算为 δr米,δH米。试求反应堆的初始反应性 ρ 以及快中子不泄漏几率和热中子不泄漏几率。精品文档---下载后可任意编辑5.一个球壳形反应堆,内半径为,外半径为,假如球的内、外均为真空,求证单群理论的临界条件为:解答:以球心为坐标原点建立球坐标系,单群稳态扩散方程:边界条件:i. ii. (假如不包括了外推距离的话,所得结果将与题意相悖)球域内方程通解:由条件 i 可得:由条件 ii 可得:由此可见,,证毕。7.一由纯金属组成的球形快中子堆,其周围包以无限厚的纯,试用单群理论计算其临界质量,单群常数如下:。解:以球心为左边原点建立球左边系,对于 U-235 和 U-238 分别列单群稳态扩散方程,设其分界面在半径为 R处:方程 1方程 2边界条件:i. ii. iii. iv.令(.在此临界条件下,既等于材料曲率,也等于几何曲率),球域内方程 1 通解:由条件 i 可知,所以:球域内方程 2 通解:由条件 iv 可知,所以:由条件 ii 可得:由条件 iii 可得:所以(由题目已知参...