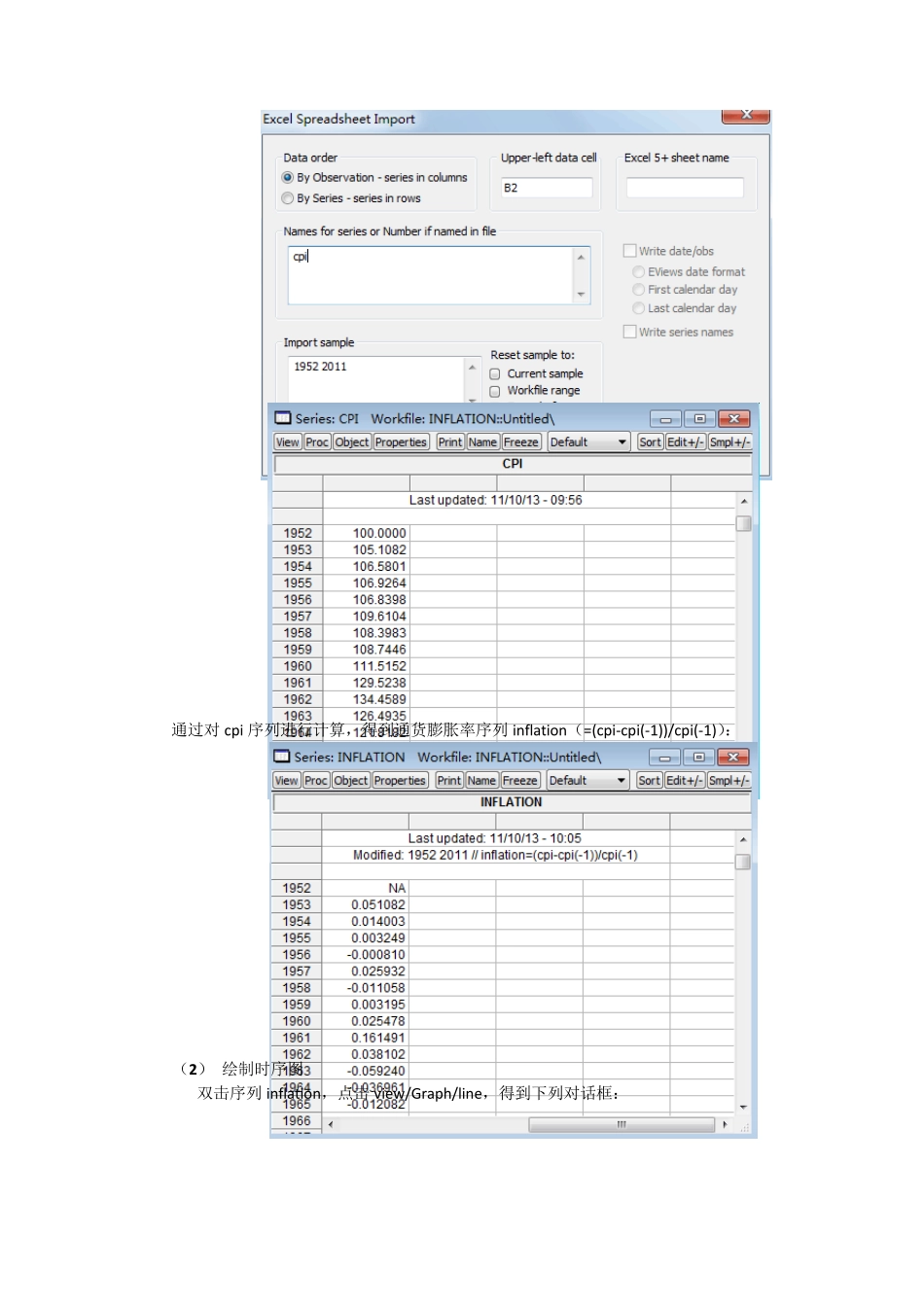
实验指导书(ARMA模型建模与预测) 例1 :我国1 9 5 2 -2 0 1 1 年的通货膨胀率数据建模及预测 注:从国家统计局网站上下载到的cpi 是以上一年为100 计算的消费价格指数,即环比数据;而1952 年为基期的消费价格指数的计算,需要借助环比发展速度与定基发展速度的关系来得到。 (1 )数据录入 打开Eviews 软件,选择“File”菜单中的“New--Workfile”选项,在“Workfile structure type” 栏 选择“Dated –regular frequency” ,在 “Date specification” 栏 中 分 别 选择“Annual”(年数据) ,分别在起始年输入1952,终止年输入2011,文件名输入“cpi”,点击 ok,见下图,这样就建立了一个工作文件。 在 workfile 中新建序列 cpi,并录入数据(点击 File/Import/Read Text-Lotus-Excel…, 找到相应的Excel 数据集,打开数据集,出现如下图的窗口,在“Data order”选项中选择“By observation-series in columns”即按照观察值顺序录入,第一个数据是从B2 开始的,所以在“Upper-left data cell”中输入B2,本例只有一列数据,在“Names for series or number if named in file”中输入序列的名字 cpi,点击 ok,则录入了数据): 通过对cpi 序列进行计算,得到通货膨胀率序列inflation(=(cpi-cpi(-1))/cpi(-1)): (2 ) 绘制时序图 双击序列inflation,点击view /Graph/line,得到下列对话框: 选择图形类型,就可绘制下图的序列时序图,时序图看出1953-2011 年的通货膨胀率数据是平稳的,这个判断比较粗糙,需要用统计方法进一步验证。 -.10-.05.00.05.10.15.20.25556065707580859095000510INFLATION 在进一步分析之前,先将序列零均值化,生成新的序列x=inflation-@mean(inflation),x序列及其序列图如下图所示,后面的分析将围绕 x 序列进行分析。 -.10-.05.00.05.10.15.20.25556065707580859095000510X (3)绘制序列相关图 双击序列x,点击view/Correlogram,出现下图对话框, 我们对原始数据序列做相关图,因此在“Correlogram of”对话框中选择“Level”即表示对原始序列做相关,在滞后阶数中选择 12(或 8=60 ),点击ok,即出现下列相关图: 从相关图看出,自相关系数迅速衰减为 0,说明序列平稳,但最后一列白噪声检验的 Q统计量和相应的伴随概率表明序列存在相关性,因此序列为平稳非白噪声序列。我们可以对序列采用 Box-Jen...