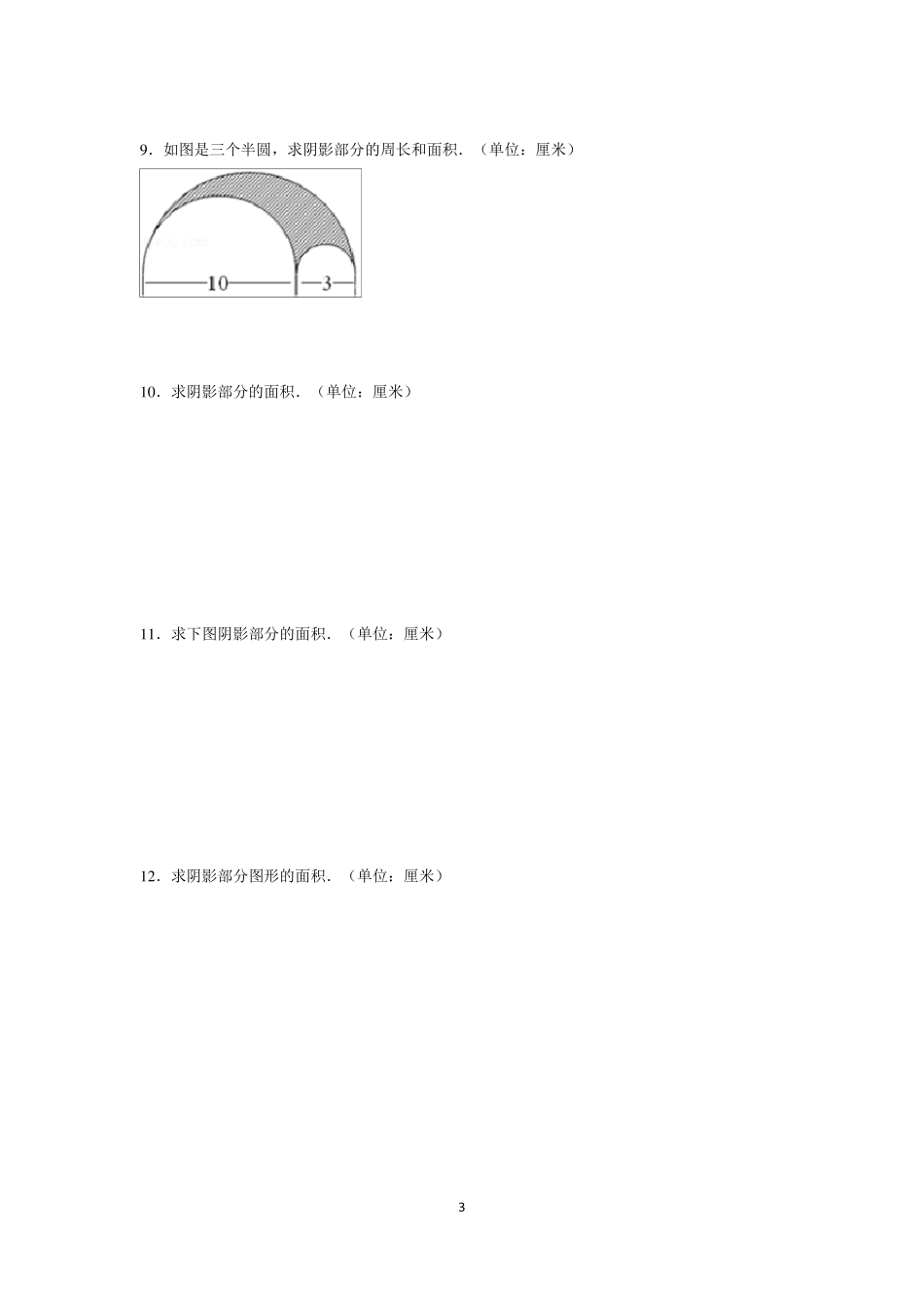
1 小升初阴影部分面积专题 1 .求如图阴影部分的面积.(单位:厘米) 2 .如图,求阴影部分的面积.(单位:厘米) 3 .计算如图阴影部分的面积.(单位:厘米) 4 .求出如图阴影部分的面积:单位:厘米. 2 5 .求如图阴影部分的面积.(单位:厘米) 6 .求如图阴影部分面积.(单位:厘米) 7 .计算如图中阴影部分的面积.单位:厘米. 8 .求阴影部分的面积.单位:厘米. 3 9 .如图是三个半圆,求阴影部分的周长和面积.(单位:厘米) 1 0 .求阴影部分的面积.(单位:厘米) 1 1 .求下图阴影部分的面积.(单位:厘米) 1 2 .求阴影部分图形的面积.(单位:厘米) 4 1 3 .计算阴影部分面积(单位:厘米). 1 4 .求阴影部分的面积.(单位:厘米) 1 5 .求下图阴影部分的面积:(单位:厘米) 1 6 .求阴影部分面积(单位:厘米). 1 7 .(2 0 1 2 •长泰县)求阴影部分的面积.(单位:厘米) 5 参考答案与试题解析 1.求如图阴影部分的面积.(单位:厘米) 考点: 组合图形的面积;梯形的面积;圆、圆环的面积. 分析: 阴影部分的面积等于梯形的面积减去直径为 4 厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答. 解答: 解:(4+6)×4÷2÷2﹣3.14×÷2, =10﹣3.14×4÷2, =10﹣6.28, =3.72(平方厘米); 答:阴影部分的面积是 3.72 平方厘米. 点评: 组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用. 2.如图,求阴影部分的面积.(单位:厘米) 考点: 组合图形的面积. 分析: 根据图形可以看出:阴影部分的面积等于正方形的面积减去 4 个扇形的面积.正方形的面积等于(10×10)100 平方厘米,4 个扇形的面积等于半径为(10÷2)5 厘米的圆的面积,即:3.14×5×5=78.5(平方厘米). 解答: 解:扇形的半径是: 10÷2, =5(厘米); 10×10﹣3.14×5×5, 100﹣78.5, =21.5(平方厘米); 答:阴影部分的面积为 21.5 平方厘米. 点评: 解答此题的关键是求4 个扇形的面积,即半径为 5 厘米的圆的面积. 6 3.计算如图阴影部分的面积.(单位:厘米) 考点: 组合图形的面积. 分析: 分析图后可知,10 厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半...