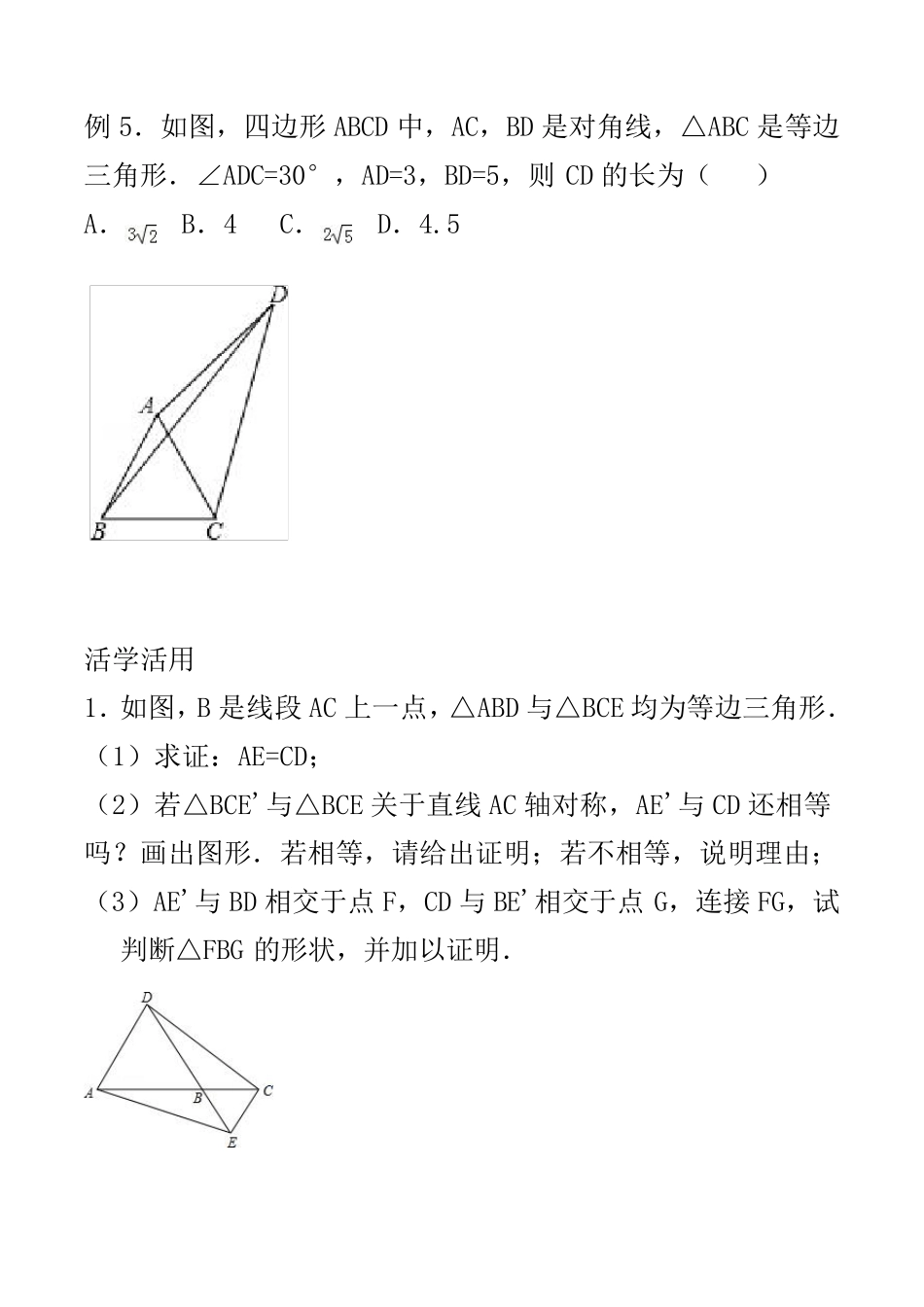
课程主题:全等三角形的常见模型授课时间:学习目标 1、掌握全等三角形的常见模型:手拉手模型、半角模型、K 字形类型一、手拉手模型例1.如图,C 为线段AE 上一动点(不与点A,E 重合),在AE同侧分别做正△ABC 和正△CDE,AD 与BE 交于点O,AD 与BC交于P 点,BE 与CD 交于点Q,连接PQ。以下五个结论:①AD=BE;②PQ∥AE③AP=BQ④DE=DP⑤∠AOB=60。下列结论恒成立的有例2.如图,分别以△ABC 的边 AB,AC 向外作等边三角形ABD和等边三角形ACE,线段BE 与CD 相交于点O,连接OA.(1)求证:BE=DC;(2)求∠BOD 的度数;(3)求证:OA 平分∠DOE.例3.已知△ABC,△ADE 均为等腰直角三角形,且∠BAC=∠DAE=90°,BD 的延长线交 AC 于点 F,交 CE 于 G.(1)求证:BD⊥CE;(2)连接 AG,求证:EG+DG= AG.例4.在锐角三角形ABC 中,AH 是 BC 边上的高,分别以 AB、AC为一边,向外作正方形ABDE 和 ACFG,连接 CE、BG 和 EG,EG与 HA 的延长线交于点 M,下列结论:①BG=CE;②BG⊥CE;③AM 是△AEG 的中线;④∠EAM=∠ABC,其中正确结论的个数是()A.4 个B.3 个C.2 个D.1 个例5.如图,四边形ABCD 中,AC,BD 是对角线,△ABC 是等边三角形.∠ADC=30°,AD=3,BD=5,则 CD 的长为()A.B.4C.D.4.5活学活用1.如图,B 是线段 AC 上一点,△ABD 与△BCE 均为等边三角形.(1)求证:AE=CD;(2)若△BCE'与△BCE 关于直线AC 轴对称,AE'与 CD 还相等吗?画出图形.若相等,请给出证明;若不相等,说明理由;(3)AE'与 BD 相交于点 F,CD 与 BE'相交于点 G,连接 FG,试判断△FBG 的形状,并加以证明.2.如果两个等边三角形△ABD 和△BCE,连接AE 与CD,证明:(1)AE 与DC 的夹角为60°;(2)AE 与DC 的交点设为H,BH 平分∠AHC.3.如图,在△ABC 中,已知∠ABC=45°,过点 C 作 CD⊥AB 于点D,过点 B 作 BM⊥AC 于点 M,CD 与BM 相交于点 E,且点 E 是 CD的中点,连接MD,过点 D 作 DN⊥MD,交 BM 于点 N.(1)求证:△DBN≌△DCM;(2)请探究线段 NE、ME、CM 之间的数量关系,并证明你的结论.4.如图,两个正方形ABCD 和DEFG,连接AG 与CE,二者相交于H 问:(1)△ADG≌△CDE 是否成立?(2)AG 是否与CE 相等?(3)AG与CE之间的夹角为多少度?(4)HD 是否平分∠AHE?(如果你知道勾股定理的话,请问线段AC、GE、AE...