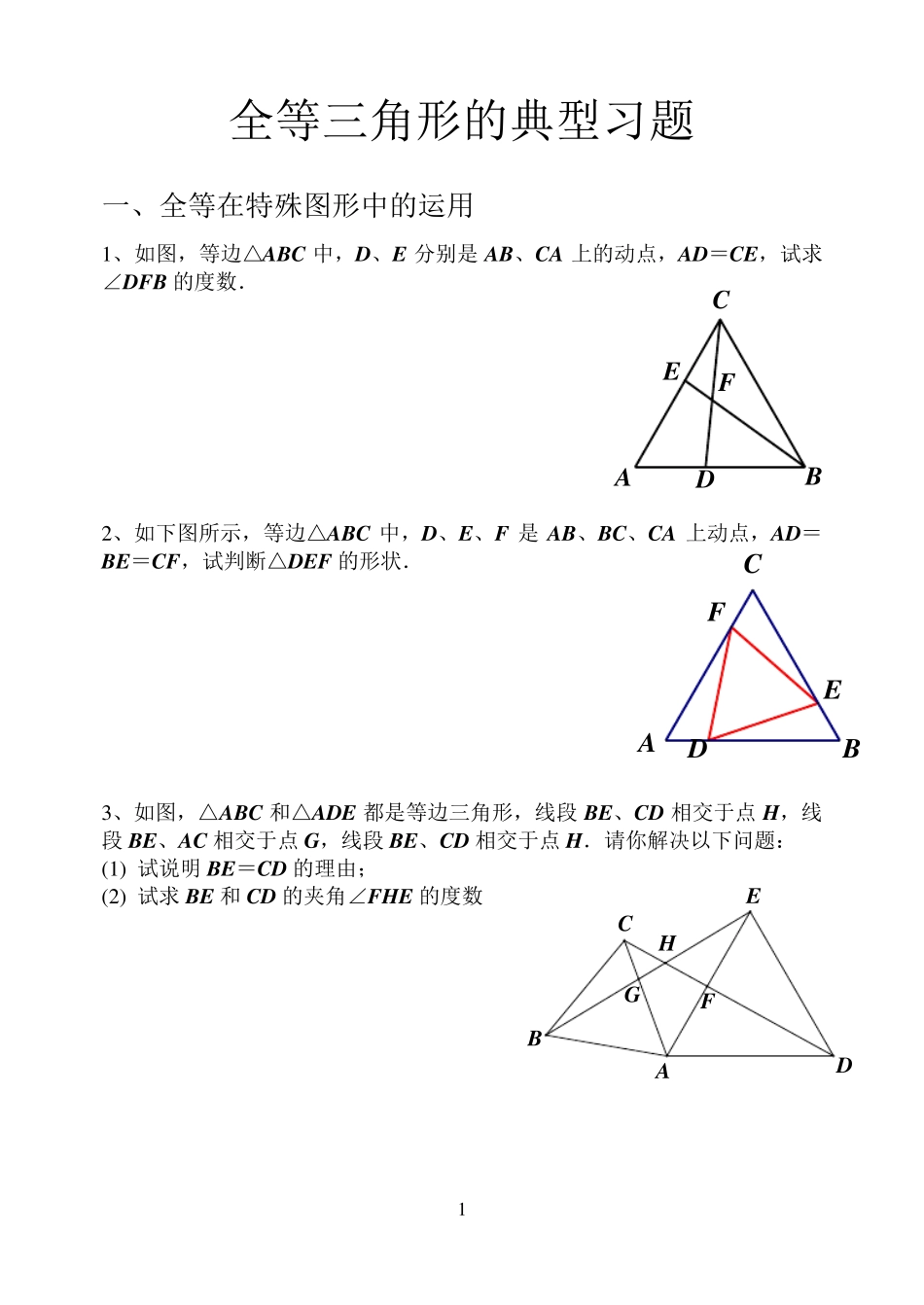
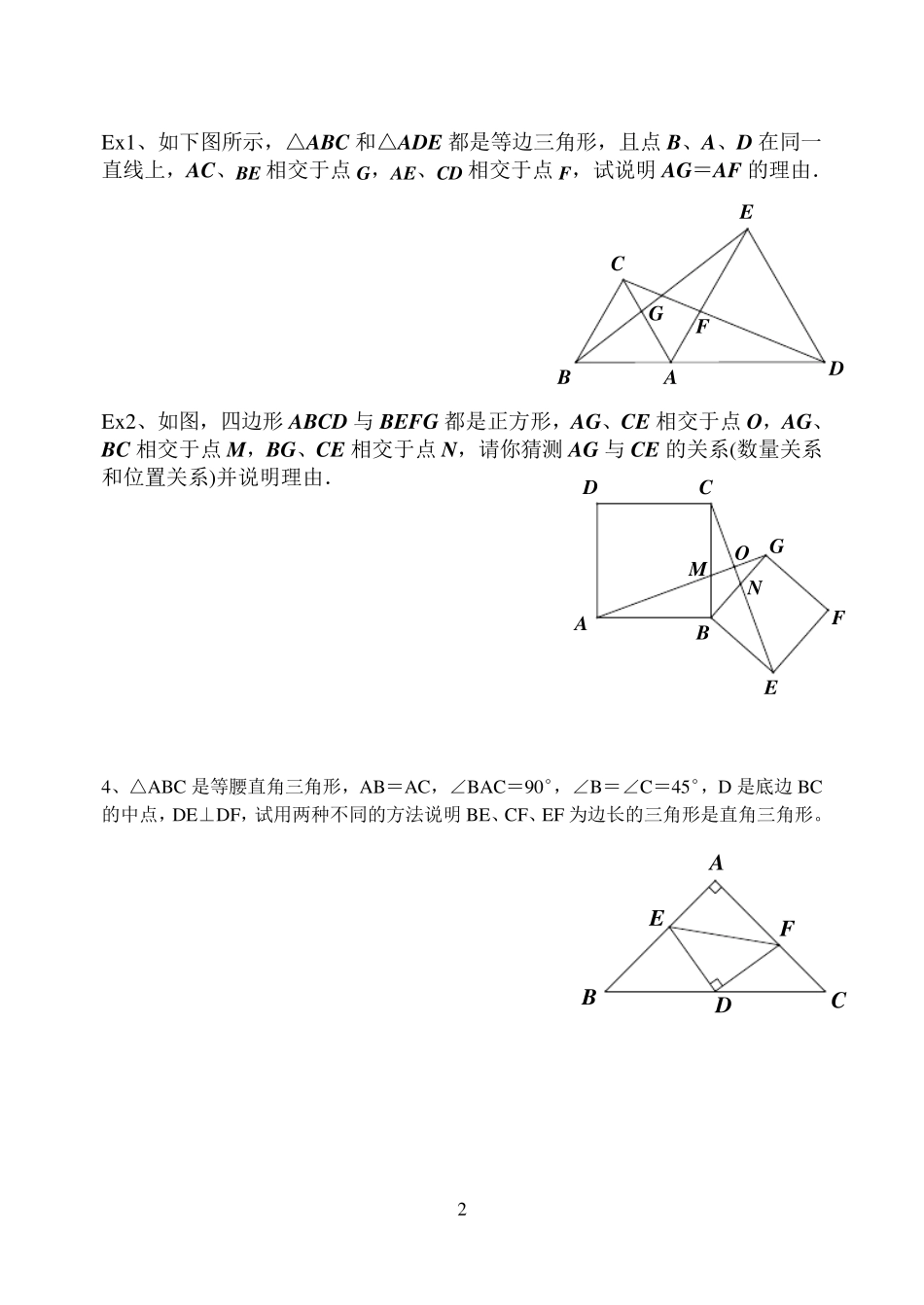
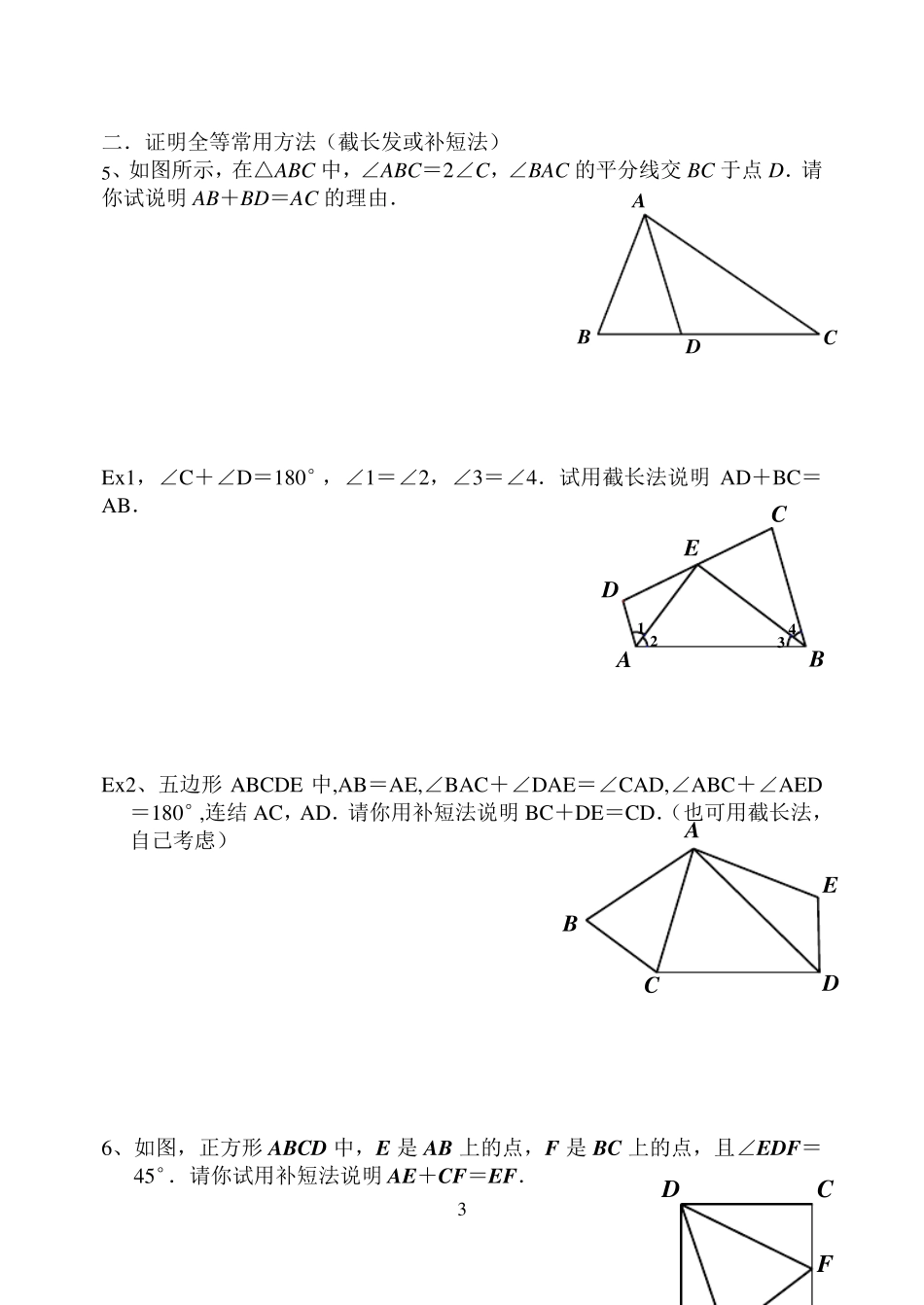
1 全等三角形的典型习题 一、全等在特殊图形中的运用 1 、如图,等边△ABC 中,D、E 分别是AB、CA 上的动点,AD=CE,试求∠DFB 的度数. 2 、如下图所示,等边△ABC 中,D、E、F 是AB、BC、CA 上动点,AD=BE=CF,试判断△DEF 的形状. 3 、如图,△ABC 和△ADE 都是等边三角形,线段 BE、CD 相交于点H,线段 BE、AC 相交于点G,线段 BE、CD 相交于点H.请你解决以下问题: (1 ) 试说明 BE=CD 的理由; (2 ) 试求BE 和 CD 的夹角∠FHE 的度数 FECABDFECABDFGHBEADC 2 FADCBE Ex1、如下图所示,△ABC 和△ADE 都是等边三角形,且点B、A、D 在同一直线上,AC、BE 相交于点G,AE、CD 相交于点F,试说明AG=AF 的理由. Ex2、如图,四边形ABCD 与BEFG 都是正方形,AG、CE 相交于点O,AG、BC 相交于点M,BG、CE 相交于点N,请你猜测AG 与CE 的关系(数量关系和位置关系)并说明理由. 4、△ABC 是等腰直角三角形,AB=AC,∠BAC=90°,∠B=∠C=45°,D 是底边BC的中点,DE⊥DF,试用两种不同的方法说明BE、CF、EF 为边长的三角形是直角三角形。 FGBEADCONMFGDABCE 3 二.证明全等常用方法(截长发或补短法) 5、如图所示,在△ABC 中,∠ABC=2∠C,∠BAC 的平分线交BC 于点D.请你试说明AB+BD=AC 的理由. Ex1,∠C+∠D=180°,∠1=∠2,∠3=∠4.试用截长法说明AD+BC=AB. Ex2、五边形 ABCDE 中,AB=AE,∠BAC+∠DAE=∠CAD,∠ABC+∠AED=180°,连结 AC,AD.请你用补短法说明BC+DE=CD.(也可用截长法,自己考虑) 6、如图,正方形 ABCD 中,E 是 AB 上的点,F 是 BC 上的点,且∠EDF=45°.请你试用补短法说明AE+CF=EF. 3421CEABDBADCEDABCFCD 4 mNMDEGFABC Ex1.、如图所示,在△ABC 中,边BC 在直线m 上,△ABC 外的四边形ACDE和四边形ABFG 均为正方形,DN⊥m 于N,FM⊥m 于M.请你说明BC=FM+DN 的理由.(分别用截长法和补短法) (连结GE,你能说明S△ABC=S△AGE吗?) 三.全等在探究题中的运用 7、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF,且EF 交正方形外角DCG的平行线CF 于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB 的中点M,连接ME,则AM=EC,易证AMEECF△≌△,所以AEEF. (1) 请你写出说明△ABC≌△ECF 的理由; 在此基础上...