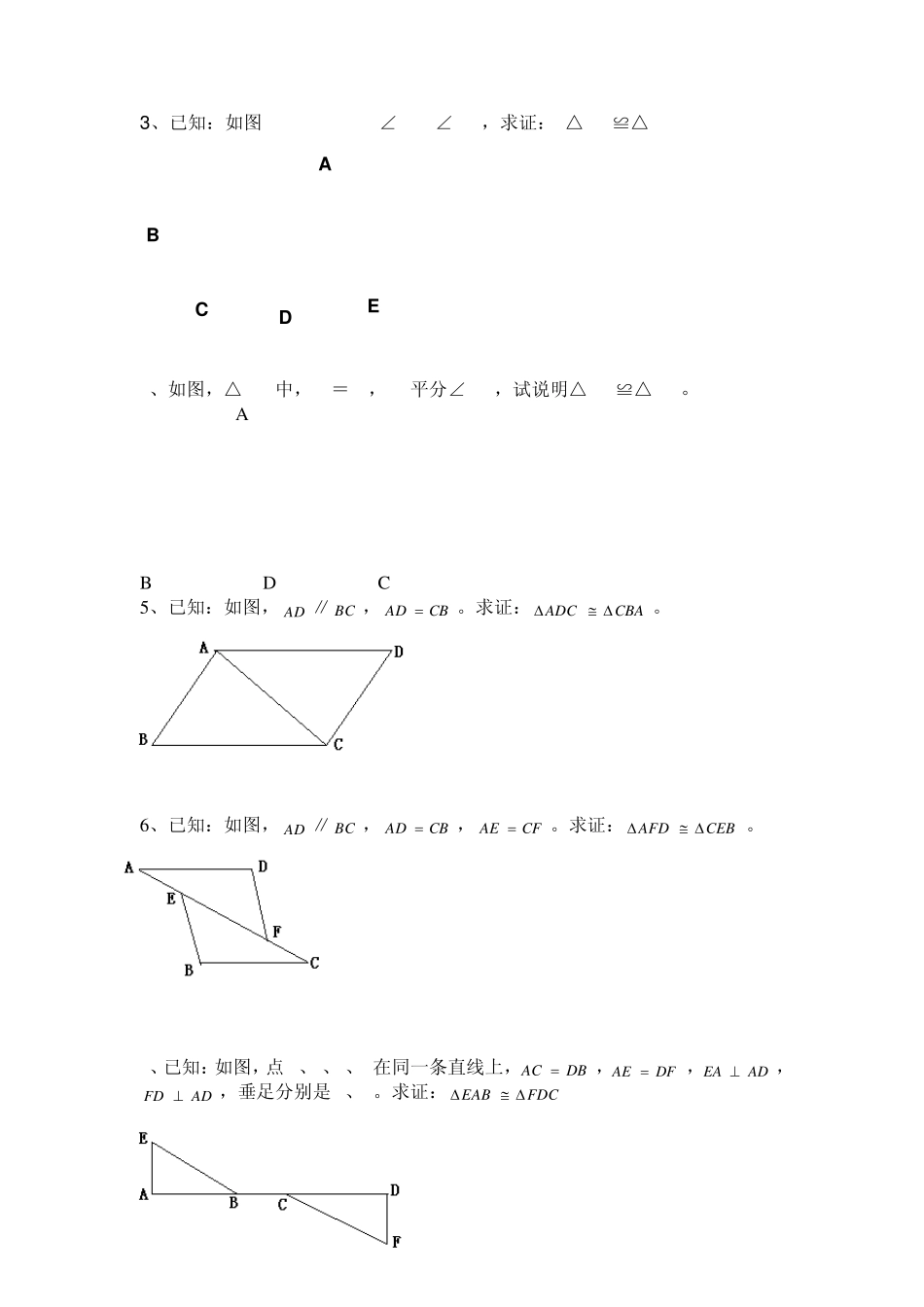
全等三角形边角边判定的基本练习 1、 如图2,AC、BD相交于O,AO、BO、CO、DO的长度如图所标,△ABO和△CDO是否能完全重合呢? 猜想: 如果两个三角形有两边和它们的夹角对应相等,那么这两个三角形 。 2、上述猜想是否正确呢?不妨按上述条件画图并作如下的实验: (1)读句画图:①画∠DAE=45°,②在AD、AE上分别取 B、C,使 AB=3.1cm , AC=2.8cm 。③连结BC,得△ABC。④按上述画法再画一个△A'B'C'。 (2)把△A'B'C'剪下来放到△ABC上,观察△A'B'C'与△ABC是否能够完全重合? 3、边角边公理. (简称“边角边”或“SAS”) 一、例题与练习 1、填空: (1)如图3,已知AD∥BC,AD=CB,要用边角边公理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是___________;还需要一个条件_____________(这个条件可以证得吗?)。 (2)如图4,已知AB=AC,AD=AE,∠1=∠2,要用边角边公理证明△ABD≌ACE,需要满足的三个条件中,已具有两个条件:一是_ _ _ _ _ _ _ _ _ _ _ ,二是 ____________还需要一个条件________________(这个条件可以证得吗?)。 2、例1 、已知:AD∥BC,AD= CB(图3)。求证:△ADC≌△CBA. 问题:如果把图3中的△ADC沿着CA方向平移到△ADF的位置(如图5),那么要证明△ADF≌ △CEB,除了AD∥BC、AD=CB的条件外,还需要一个什 么条件(AF= CE或AE =CF)?怎样证明呢? 例2 、已知:AB=AC、AD=AE、∠1=∠2(图4)。求证:△ABD≌△ACE。 练习: 1、已知:如图,AB=AC,F、E分别是AB、AC的中点。求证:△ABE≌△ACF。 2、已知:点A、F、E、C在同一条直线上, AF=CE,BE∥DF,BE=DF. 求证:△ABE≌△CDF. ABCDE3、已知:如图AB=AC,AD=AE,∠BAC=∠DAE,求证: △ABD≌△ACE 4、如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD。 A B D C 5、已知:如图, AD ∥ BC ,CBAD 。求证:CBAADC。 6、已知:如图, AD ∥ BC ,CBAD ,CFAE 。求证:CEBAFD。 7、已知:如图,点 A、B、C、D在同一条直线上,DBAC ,DFAE ,ADEA ,ADFD ,垂足分别是 A、D。求证:FDCEAB 8、已知:如图,ACAB ,AEAD , 21。求证:ACEABD。 9、如图,在ABC中,D 是AB 上一点,DF 交AC 于点E ,FEDE ,CEAE ,AB 与CF 有什么位置关系?说明你判断的...