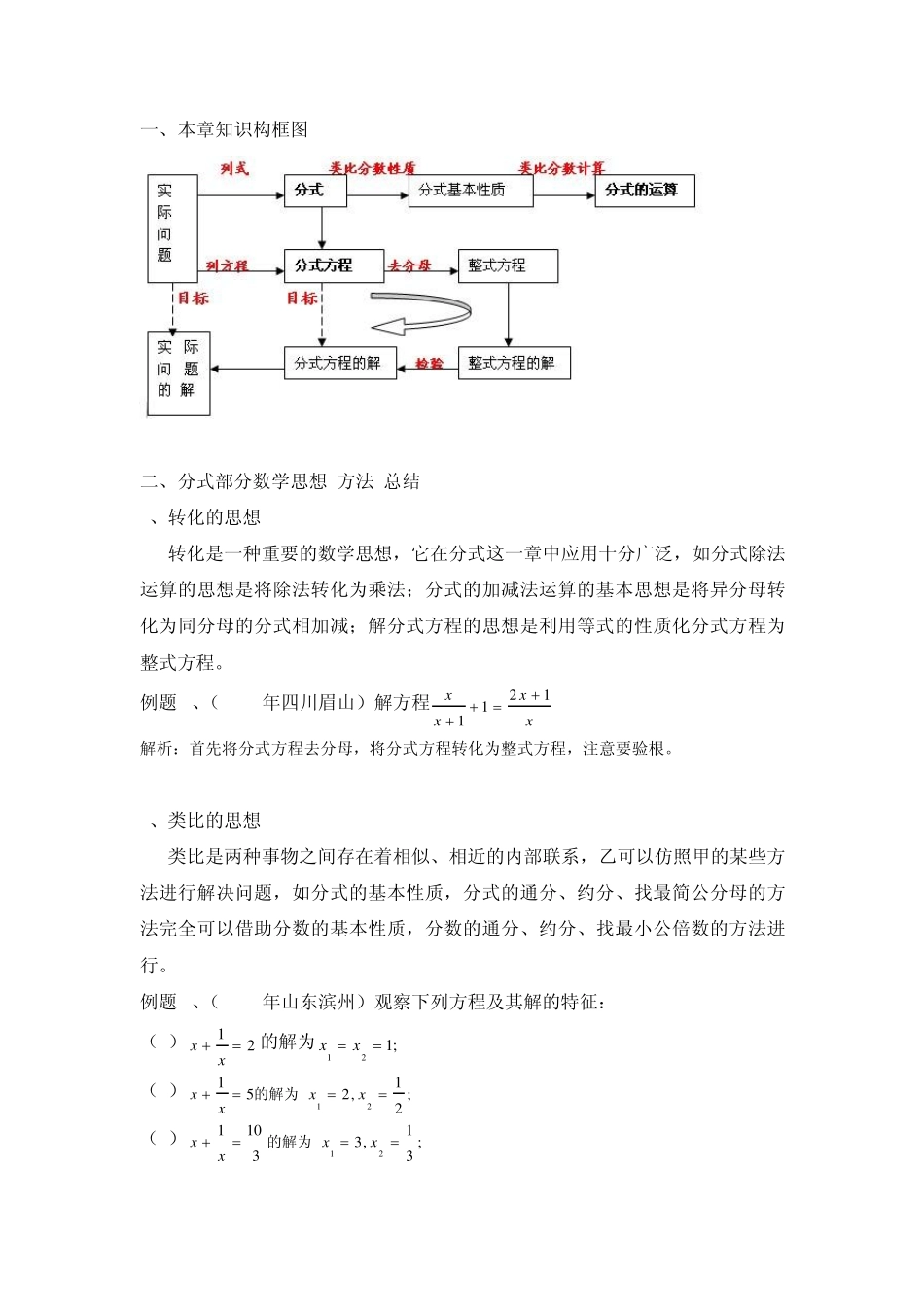
一、本章知识构框图 二、分式部分数学思想.方法.总结 1、转化的思想 转化是一种重要的数学思想,它在分式这一章中应用十分广泛,如分式除法运算的思想是将除法转化为乘法;分式的加减法运算的基本思想是将异分母转化为同分母的分式相加减;解分式方程的思想是利用等式的性质化分式方程为整式方程。 例题 1、(2010年四川眉山)解方程xxxx1211 解析:首先将分式方程去分母,将分式方程转化为整式方程,注意要验根。 2、类比的思想 类比是两种事物之间存在着相似、相近的内部联系,乙可以仿照甲的某些方法进行解决问题,如分式的基本性质,分式的通分、约分、找最简公分母的方法完全可以借助分数的基本性质,分数的通分、约分、找最小公倍数的方法进行。 例题 2、(2009年山东滨州)观察下列方程及其解的特征: (1)21 xx的解为;121 xx (2);21,25121xxxx的解为 (3);31,3310121xxxx的解为 ...... ...... 解答下列问题: (1)请猜想:方程;_ _ _ _ _ _ _ _ _ _5261的解为xx (2)请猜想:关于x的方程);0(1,_ _ _ _ _ _ _ _121aaxaxxx的解 (3)下面以解方程。)中猜想结论的正确性为例,验证(15261 xx 解析:此题是一类阅读解答题,用类比的方法进行解答 3、整体思想 给出一定的条件,在此条件下求分式的值称为有条件的分式求值,解有条件的分式求值问题时,既要瞄准目标,又要抓住条件,找出条件与待求式之间的内在联系即找准切入点,解题时经常用到整体换思想。 例题3、(1)已知;3434,511babababbba求 (2)已知baababab,)(2911求的值. 解析:(1)把已知条件转化为所求分式所需要的形式,由511ba,可得 a-b=-5ab,把a-b=-5ab,整体代入所求分式。 (2)把所求分式变形,条件随所求分式变形后的结果而改变; 4、数形结合的思想 利用几何图形(数轴)建立方程求解,在近几年中考中越来越明显。 三、专题讲座 专题一、分式求值中得一些解题技巧 专题概说:分式的四则运算的理论依据就是分式的基本性质和一些数学公式,有时灵活运用条件,巧妙变形,能使计算(化简)过程异常简洁。 例题1:(2011年黄冈实验中学模拟题)已知实数a、b满足ab=1,那么111122ba的值为______________. 解析:直接使用 ab=1比较困难,巧妙地运用分式基本性质进行等值变形,再根据 ab=1代换。 例题 2:(2011年黄州城区联考...